中国指挥与控制学会会刊 
作为远距离、全天时和全天候使用的传感器,雷达在海空目标探测和监视方面得到了广泛应用。为覆盖一定的区域范围,通常将多部雷达数据组网融合处理。雷达组网的重要研究方向是阵地部署优化问题,该问题可表述为:给定多个候选阵地条件下,通过设计优化目标和约束条件,采用特定优化算法求解传感器最优部署位置。常见的优化算法包括遗传算法、粒子群算法和差分进化算法等。其中,遗传算法作为启发式搜索算法,优化目标不要求连续,且具备较强的并行性,可实现单值目标函数(或转化为单值目标)的优化求解,在组网部署优化问题中得到广泛应用。
杨仕明等[1]在建立多指标加权优化目标的基础上,采用遗传算法,进行雷达组网部署优化研究。黄胡晟等[2]采用类似目标函数,针对N部雷达部署到N个阵地进行染色体编码。刘帅等[3]针对民航雷达组网的部署优化问题,提出采用带精英选择策略的遗传优化算法。张远等[4]提出了综合考虑多种因素的雷达组网目标优化函数,并采用基于非二进制编码的遗传算法求解部署策略。宋佳庆[5]、付鑫等[6]利用遗传算法求解反导装备的部署优化问题,在目标函数定义方面与对空雷达组网探测的差别较大。
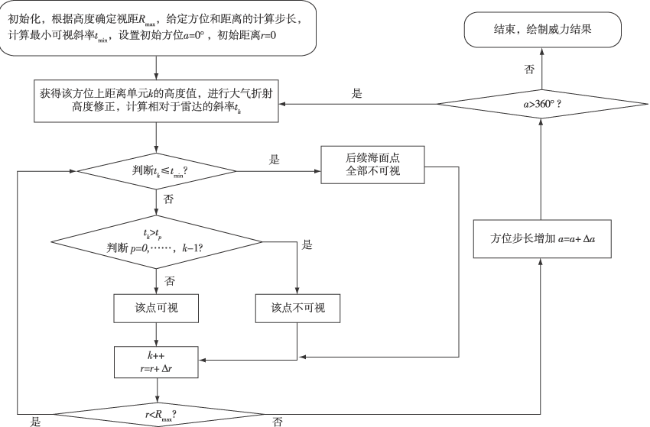
然而,上述研究均未考虑实际地形对雷达网探测的影响。由于高程对雷达的探测威力影响很大,实际部署应加以考虑。给定高程数据下,王中杰等[7-8]利用实际部署时应考虑的多个约束条件来减少遗传算法寻优范围。潘伟等[9]提出了基于自适应步长的改进遗传算法求解雷达网最优部署。梅发国等[10]在考虑一定部署约束条件下,将遗传算法应用于大规模对空雷达组网部署优化问题。针对实际的地形数据,上述文献均采用雷达地理位置进行染色体编码,并采用雷达探测盲区的地形遮挡模型。如吴强等[11]提出基于高程数据的雷达探测盲区建模,薛宏涛等[12]利用相邻角度相关性的转盘爬虫算法来提高对雷达盲区的建模速度。周宗伟等[13]结合雷达垂直威力图和数字高程数据,对不同高度层上的雷达遮蔽盲区进行建模。陈超凡等[14]提出大气折射修正下的雷达遮蔽盲区建模方法。王栋等[15]基于SRTM(Shuttle Radar Topography Mission,航天飞机雷达地形测绘使命)高程数据,在对大气折射修正基础上,提出了变步长对海雷达威力建模方法,该方法可减小计算量。
以上基于地形数据的威力或遮挡盲区的建模,均是将雷达探测角度和距离范围进行格点化处理后,针对每个方位上所有距离单元,计算雷达相对目标的视线上是否存在遮蔽,因而计算复杂度较高。而基于实际地形,采用遗传算法部署优化研究[7⇓-9],均将雷达地理位置进行染色体编码,在每次迭代求解适应度函数(即优化目标函数)时,需要求解所有待部署雷达的威力模型,导致优化算法的复杂度更高。如王中杰等[7]虽然采用综合考虑多个部署约束条件简化算法的寻优空间后,部署4部雷达仍需要小时量级的时间,因此,有必要研究针对实际地形的快速优化求解方案。
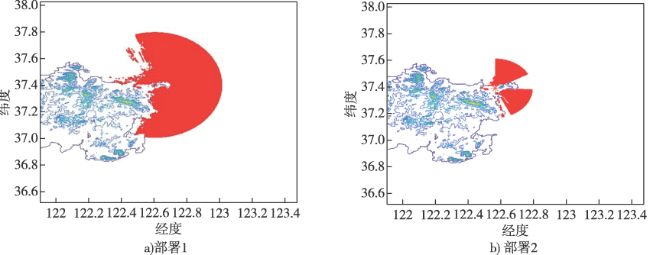
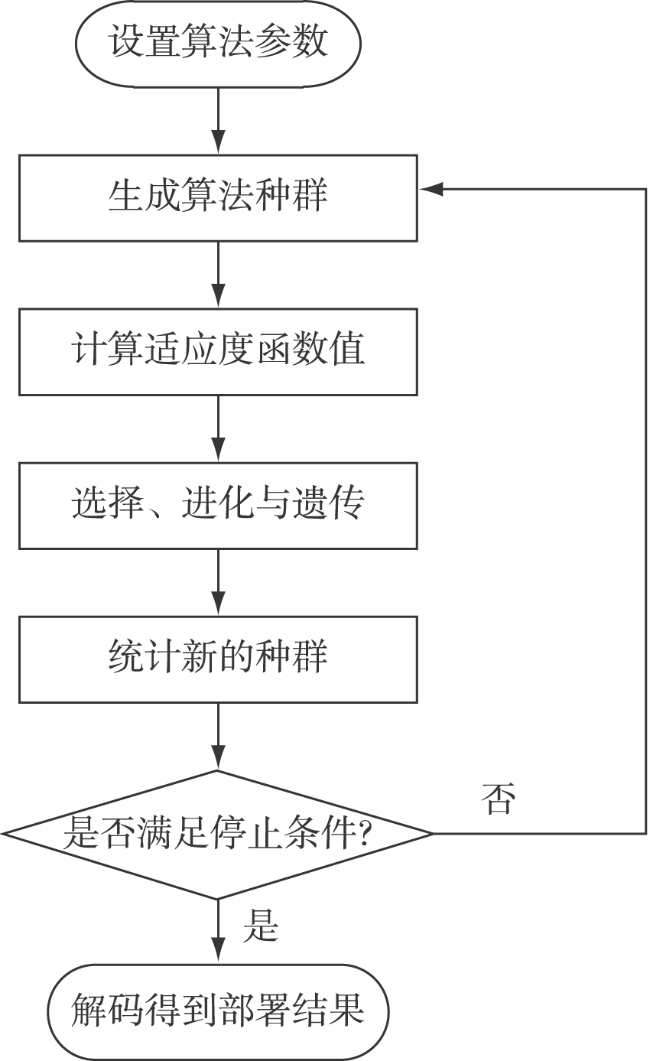
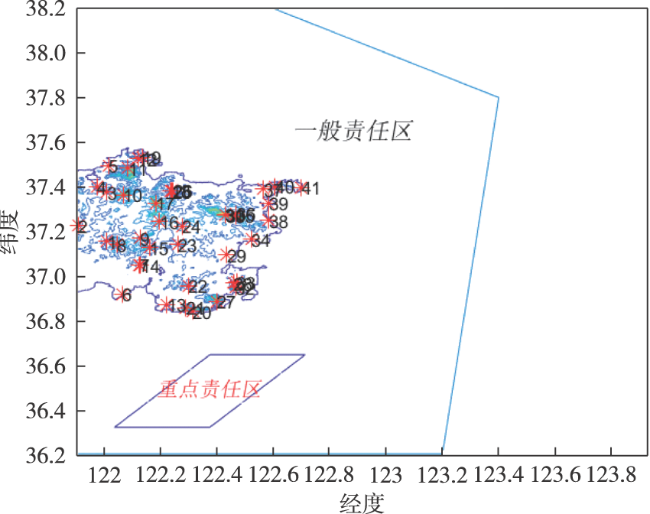
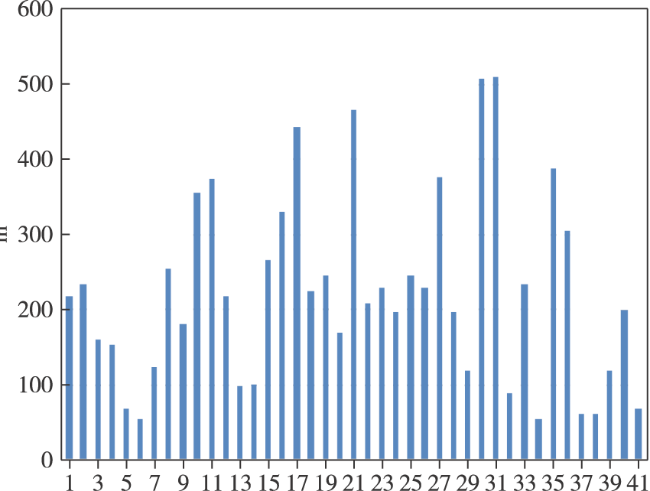
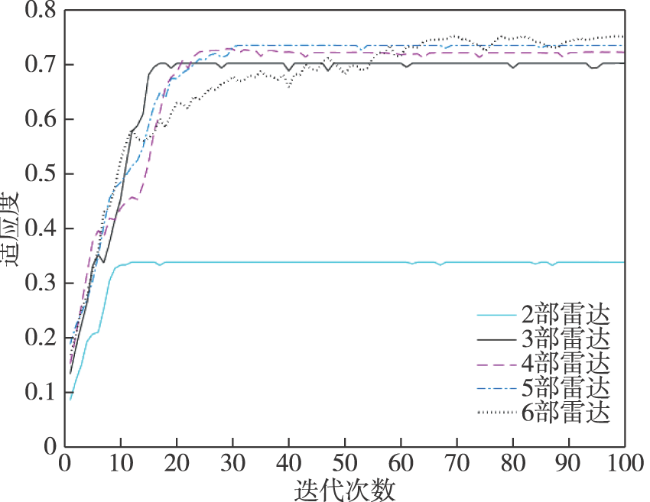
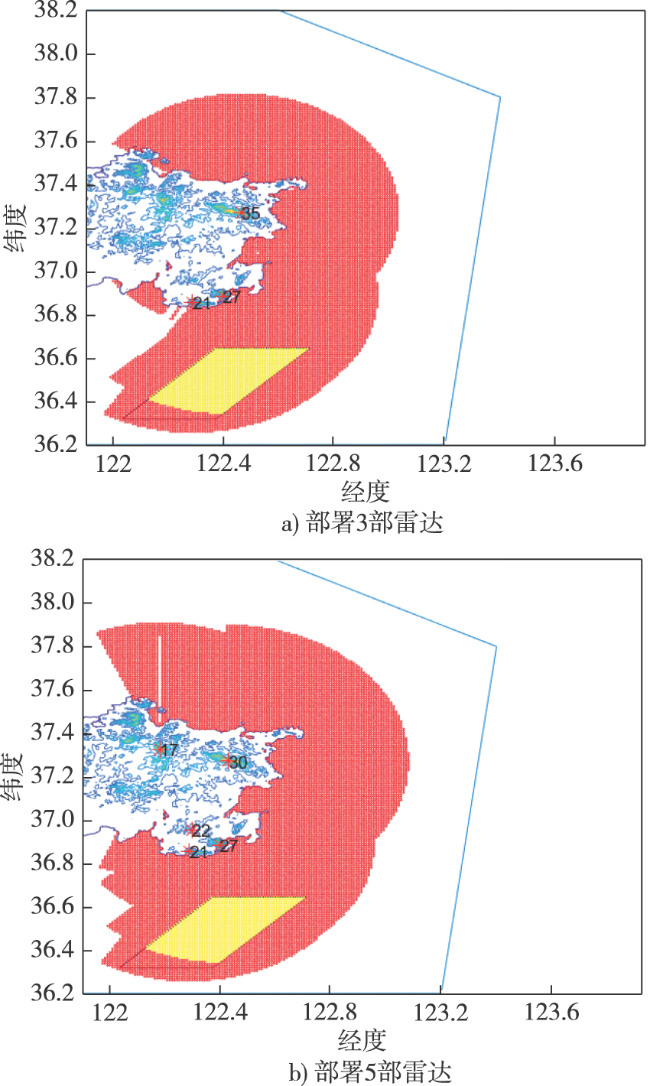
在对海探测应用场景中,雷达威力主要受视距限制,通常选择局部地形的最高点(沿海山头)作为待部署的阵地,利用该先验信息可极大减小遗传优化的求解空间,只需针对上述待部署阵地进行优化即可。具体来说,首先利用对海雷达探测威力模型,计算备选阵地在实际高程数据下的威力范围,并以阵地编号索引存储,然后,采用遗传算法对备用阵地进行二进制编码,再利用离线存储阵地的威力数据,求解适应度函数得到最优部署方案。该方法可灵活满足实际待部署阵地的各种现实要求,同时,可极大提升优化算法的求解效率。
1 对海雷达威力模型
本研究所用的原始地形数据格式为带高程信息的矩阵,按照经度、纬度和高度三列进行存储,矩阵中每一行对应实际地理位置的一个格点,记录对应点经度、纬度和高度。在数据预处理阶段,读取原始地形数据存储至地面坐标系高程数据矩阵,矩阵行和列对应格点的纬度和经度坐标,经度和纬度网格数据的步长均为120 m。
高程对雷达威力模型的影响主要体现在两方面。一是影响雷达的最大作用距离——视距。由于警戒雷达接收海上目标的灵敏度相对视距足够大,本文假定对海雷达的最大距离通常仅受视距影响。二是地形起伏造成在某些方向上雷达威力的缩减,即存在雷达的威力盲区,此时,对海雷达威力不再是理想的圆形,而是在不同角度上有起伏。
本文采用文献[15]给出的对海探测威力计算模型。该模型既考虑了大气折射下的地形和目标高度修正,又实现了对海探测时不连续阴影区的建模。给定雷达架设位置后,假定雷达最大威力为Rmax,方位步长Δa,距离步长取高程数据步长Δr(该值太大则不能有效利用数据,太小则受到高程数据步长限制,不能提升性能却增加计算量,因此,取高程数据步长),则距离单元格数为T=R/Δr。基于实际地形数据的对海雷达探测威力的计算流程如图1 所示。
从算法流程可以看出,每个方位需要的最大计算次数为 t=(1+T)T/2,将地形单元数据的大气折射修正、高度插值和视线斜率作为基本运算Q,则上述模型的计算复杂度可表示为
Ο((360/Δa)(Rmax/Δr)2Q)
可以看出,上述威力模型与最大作用距离、方位和距离步长均有关系。随着数据分辨率的提高,上述算法的复杂度与Δr成2次幂增加的关系,因此,该算法具有较高复杂度。
基于上述威力计算模型,对山东半岛东北角的两相邻的位置点(部署1阵地经纬度为122.60E, 37.40N,部署2阵地经纬度为122.56E, 37.39N,两点相距4.5 km)进行部署后,绘制雷达对海探测威力如图2 所示。经统计,部署1对海域的覆盖面积为部署2对海域的覆盖面积的4倍左右。因此,对海雷达探测威力受到部署阵地高度和周边的地形影响很大。为获得尽量大的海上探测威力范围,我们应选择沿海的局部制高点。
2 部署优化问题模型
上文给出了对海探测威力模型,得到的威力数据可用威力指示矩阵来存储。该矩阵每行对应雷达某个角度的探测数据,每列代表某个距离单元的探测数据。元素值为1,表示对应的经纬度格点被部署雷达威力所覆盖,值为0,则表示该点为雷达探测盲区。
除威力模型外,求解部署优化问题还需明确优化目标函数。通常对空部署优化问题表示为对不同高度层的威力覆盖度占整个责任空域的比值,而责任空域通常是根据警戒任务确定。受海上视距的影响,对海雷达网探测的范围通常为沿海区域,并尽量向外海扩展。因此,设置将沿海一定范围的海面作为观察的一般责任区,而用该覆盖范围内的规则多边形来表示重点责任区。上述责任区也可用指示矩阵来表示,指示矩阵行和列分别对应海域某格点的纬度和经度,相应矩阵元素值取1,表示部署在责任区内部,值取0表示未部署在责任区内部。
在定义责任区的基础上,可进一步定义优化目标函数。已有的对空雷达组网优化的目标函数通常为不同高度层的雷达网威力覆盖的加权和[3]。由于对海探测只有海面高度,相当于对空探测的零高度层,对海探测采用雷达网对不同责任区域的威力覆盖度加权和作为优化目标函数。我们将一般责任区的覆盖度定义为一重以上覆盖所占责任区面积的比例,而重点责任区定义为二重以上覆盖面积所占比例。假定部署N部雷达,Si为第i部雷达对责任海区的覆盖面积,i=1,2,…,N,St为责任区域面积,则一般责任区覆盖度为
α= /St
式中,∩代表两个集合的交集,∪代表集合的并集。
假定Sip、Sjp分别为第i、j部雷达对重点责任区的覆盖面积,i>j,Sp为重点责任区面积,则重点责任区覆盖度为
β= /Sp
将一般责任区和重点责任区覆盖度的加权和作为目标函数:
f(θ)=kα+(1-k)β
式中,k为加权系数,可根据一般责任区和重点责任区的重要程度灵活调整;θ为待优化的雷达部署位置。
3 遗传算法优化流程
遗传算法需要对变量进行编码,最常用的是二进制编码。由于已经得到预选阵地数M,对上述阵地编号进行染色体编码,单个雷达部署阵地的二进制编码位数为$b=\lfloor log_{2}M\rfloor$, $ \lfloor · \rfloor$代表向上取整。假定部署了N部雷达,将所有阵地的编号顺序排列,即为自变量的二进制编码,如图3 所示。
上述编码二进制数对应的分辨率为M/2b,b为二进制编码位数。译码只需将上述二进制数对应到雷达阵地编号即可。
在完成上述备选阵地威力和观察责任区的矩阵表示模型,并构建优化目标函数的基础上,针对待选阵地编码的遗传算法流程如下:
1) 首先确定部署海域的责任区表示。对上述海域高程数据进行预处理,得到观察责任区表示矩阵Τ1和Τ2,分别代表一般责任区和重点责任区。
2) 根据DEM数据,选择上述海域的M个局部最高点作为待部署点,其经纬度坐标集合为θ。选择阵地应满足以下原则:一是阵地高度不小于50 m;二是对海主要观察方向无遮蔽。显然,M越大,则得到最优解的可能性越大,通常满足M>2N,N为拟部署雷达数量。
3) 按照图1 给出的计算流程,得到上述M个阵地的对海探测威力矩阵,并存储为{Ck 。
4) 将对海责任区表示矩阵Τ1和Τ2、待部署阵地数据集合θ、阵地威力数据矩阵{Ck 代入遗传算法中进行求解,流程如图4 所示。基于备用阵地进行编码的优化算法应根据问题的规模合理设置种群数量。当备用阵地数量较小时,过大的种群数量可能会出现遍历所有可能部署的情况。当目标函数变化很小时,认为算法达到收敛,停止迭代优化。
5) 根据阵地选择的结果,绘制雷达部署位置和雷达的威力。
4 仿真结果分析
硬件环境:双频1.8 GHz的处理器和8 GB内存的单机;软件环境:Matlab R2016a。
如图5 所示,以山东半岛的地形数据为例,设置一般责任区、重点责任和41个编号阵地。一般责任区为从陆地向外扩展到蓝色线框,重点责任区为平行四边形区域,根据式(4)使两者的覆盖度加权最大,作为优化目标函数,并取k=0.5。预选阵地的高度见图6 所示。
表1 遗传算法与遍历法的性能对比Tab.1 Performance comparison between genetic algorithm and ergodic algorithm |
| 算法 | 部署雷达 | |||
|---|---|---|---|---|
| 3部雷达 | 5部雷达 | 6部雷达 | ||
| 遗传算法 | 迭代次数 | 40 | 60 | 80 |
| 时间/s | 2 470 | 5 365 | 9 038 | |
| 优化结果 (阵地编号) | 21,27,35 | 17,21,22,27,30 | 19,20,21,27,35,36 | |
| 适应度 | 0.701 1 | 0.742 9 | 0.745 9 | |
| 遍历法 | 时间/s | 14 261 | 317 152 | 886 754 |
| 优化结果 (阵地编号) | 21,27,35 | 17,21,22,27,35 | 17,20,21,27,35,36 | |
| 适应度 | 0.701 1 | 0.744 0 | 0.746 1 | |
本研究针对的是对海探测阵地选择问题,而对空探测缺少本文所描述的显著的阵地要求特征,因此,难以直接应用本文所提的方法。这里给出利用预先部署来选择备用阵地的思路:首先,将待部署区域划分成一定数量的大网格,对每个网格所有格点位置进行预先部署,通过效能对比得到该网格的最优位置作为备用阵地;然后,对上述有限的备用部署位置进行编码优化求解。需要指出,由于预先部署是对分割的区域进行对比,该方法对于雷达网来说,结果不一定最优。
5 结束语
本文基于实际高程数据,研究预先进行部署阵地选择的对海雷达组网阵地部署优化遗传算法。通过对待部署阵地编号进行二进制染色体编码,可极大提升优化求解速度。研究假定阵地的威力仅受到阵地高度和遮蔽的影响,实际上,不同体制雷达在同一阵地威力不完全相同,因此,需要进行精细的威力建模,可在本文所提的阵地威力表示矩阵模型基础上,再增加一个不同雷达类型的表示维度。另外,采用遗传算法在求解优化问题时,还受到地形分辨率、变异的步长等多个因素影响,这是我们下一步研究方向。