中国指挥与控制学会会刊 
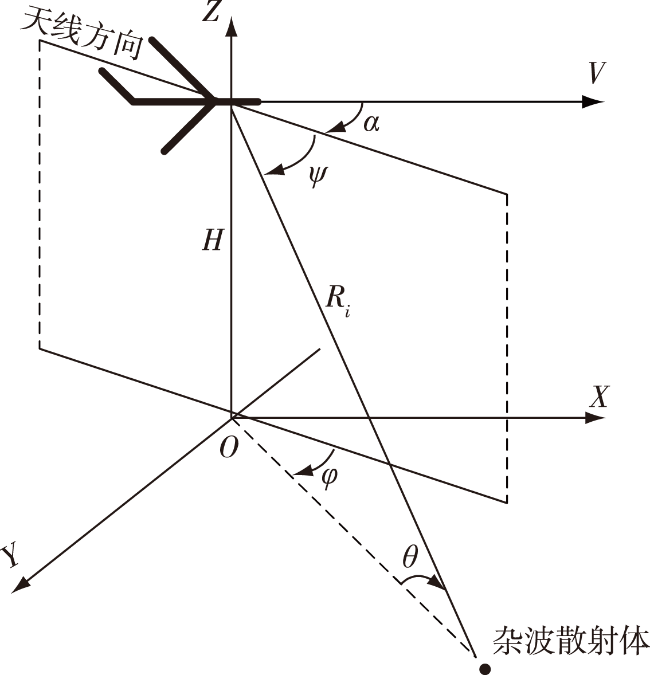
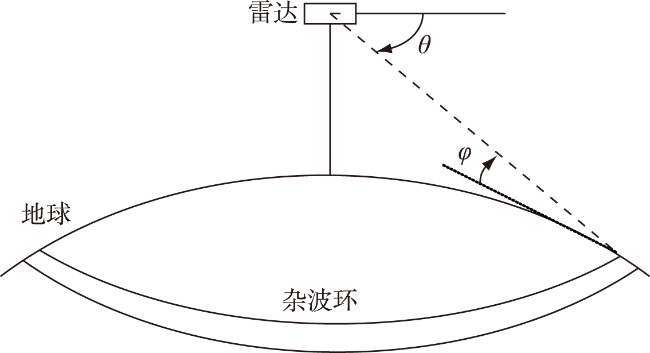
预警机将预警雷达搬上了空中平台,克服了地基雷达受地球曲率制约导致的低空盲区。机载预警雷达的主要使命之一就是探测低空突防的飞机,因此通常处于下视状态。由于平台高,速度快,地、海杂波几乎扩展到全程范围,并存在较大的多普勒频移且频谱严重展宽,目标落入杂波区后难以检测,杂波影响评估与杂波抑制方法是机载预警雷达研制中的重要课题[1]。
杂波数据的获取是评估杂波影响和验证杂波抑制方法的前提。对于机载预警雷达,组织试飞难度大,实际杂波很难采集。20世纪90年代,美国通过Mountain Top[2]和MARCAM[3]计划采集了机载预警雷达多通道杂波数据,这些数据为杂波抑制研究提供了非常有价值的依据。新一代机载预警雷达采用脉冲多普勒(PD)和有源相控阵体制[4],对于几百个数字通道来说,由于设备量和存储量有限,无法完成对每个阵元的杂波数据采集任务,机载预警雷达多通道杂波数据主要依靠仿真模拟来获得。
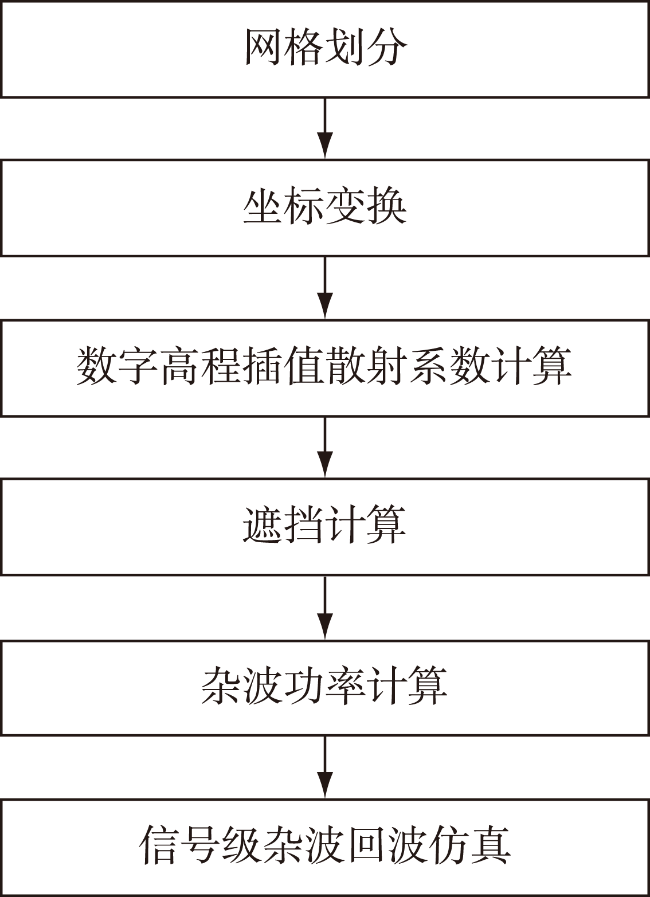
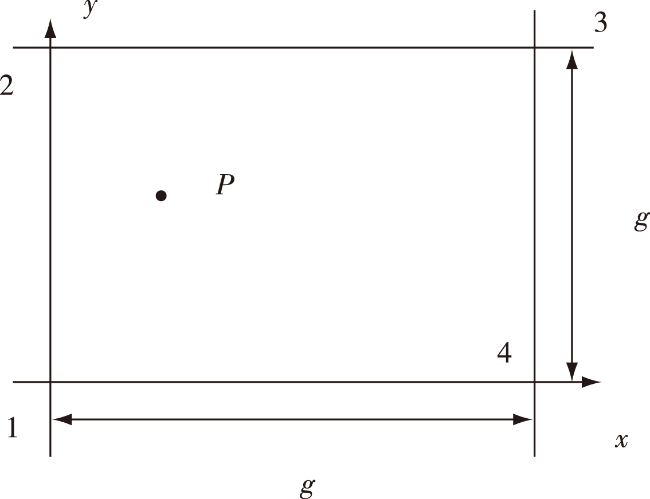
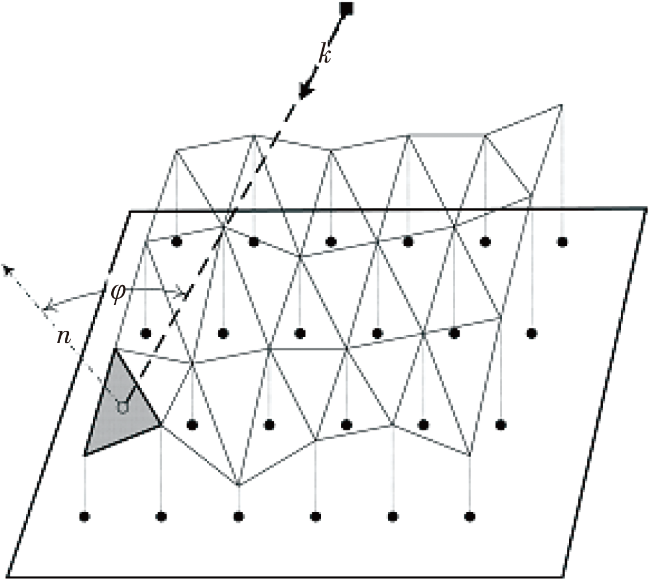
文献[5]详述了机载PD雷达的系统组成和杂波谱特征等问题,为机载PD雷达仿真提供了理论基础。文献[6]推导得到了简化杂波功率公式。文献[7]推导出了计算任意距离-多普勒网格单元杂波功率的公式,但精度较低且需要大量数值积分,限制了其工程应用。文献[8]得到了在平面地球假设下的等距离等多普勒网格单元闭合解,以等距离和等多普勒划分地面网格,解决了地表网格单元面积的问题。
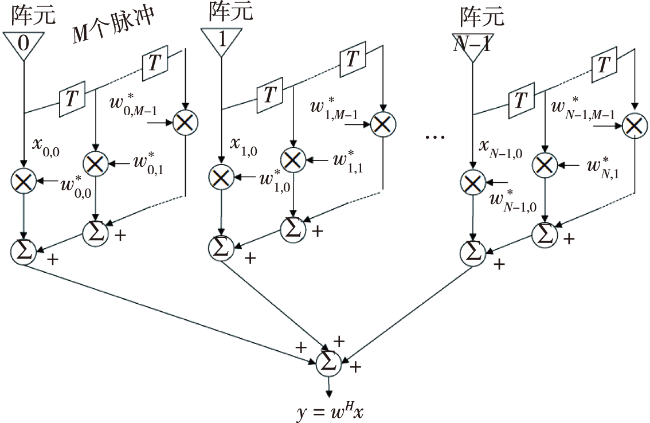
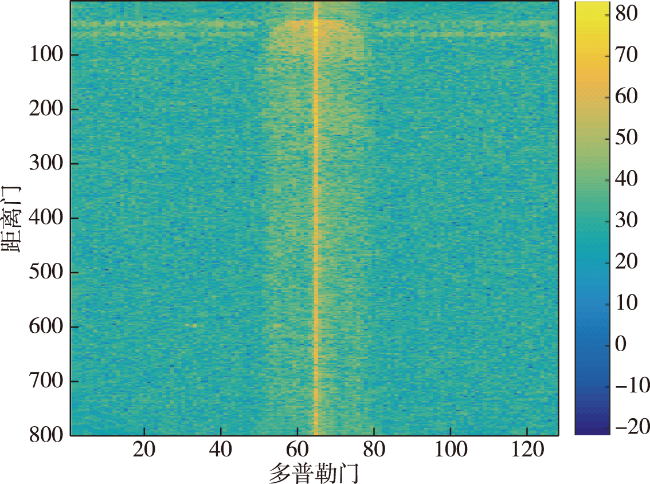
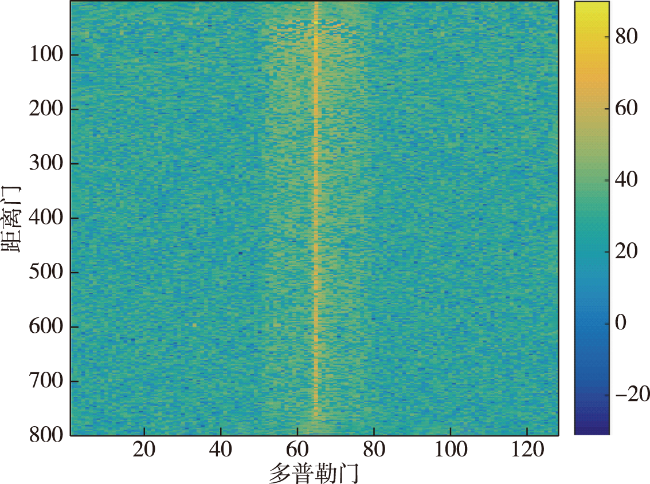
目前,机载预警雷达最为有效的杂波抑制技术是空时自适应处理技术(STAP),通过在空域时域联合自适应滤波来抑制杂波。STAP最关键的步骤是协方差矩阵的估计,而协方差矩阵应当通过待检测单元邻近的训练数据来估计。STAP处理信噪比损失小于3dB需要的均匀样本数为系统自由度的2倍。真实的环境复杂多样,地形及地表覆盖的变化引起杂波的非均匀分布,人造建筑等形成强离散杂波,密集的干扰目标污染训练样本等因素使得均匀样本严重不足,导致空时自适应性能急剧下降。
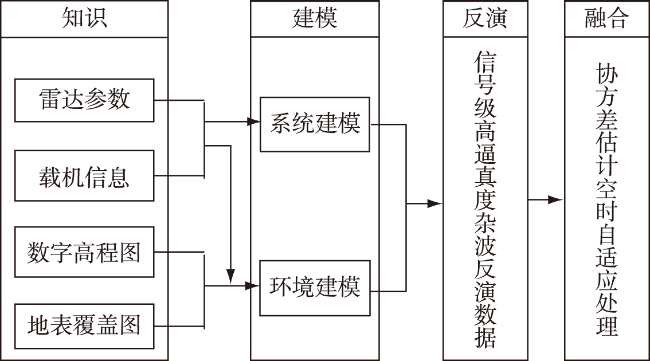
认知雷达通过感知环境和利用知识为机载预警雷达非杂波抑制提供了一种有效方法[9]。认知技术通过杂波仿真的方式增加均匀样本,改善空时自适应处理的杂波抑制性能,为杂波仿真在机载预警雷达中提供了新的应用途径。
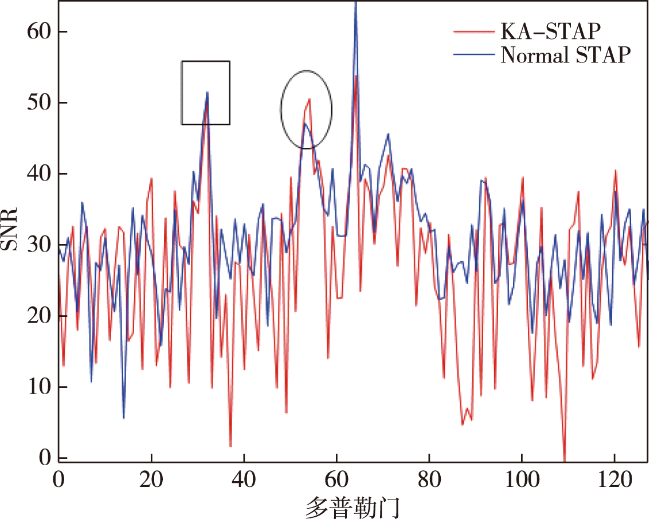
本文给出了机载预警雷达的杂波模型,介绍了STAP处理技术;介绍了一种杂波仿真的新应用,提出了基于精细化杂波仿真的认知杂波抑制技术;进行了仿真性能分析并进行了总结。
1 机载预警雷达杂波建模及STAP处理
1.1 机载预警雷达杂波建模
为了建立机载预警雷达杂波模型,给出雷达坐标系如图1 所示[10]。
假设载机高度为H,以速度V匀速运动。V平行于x轴方向,与阵面轴向夹角为α,阵面为一等距线阵,含有N个阵元,阵元间隔为d。设地面上某一散射体俯仰角为θ,方位角为ϕ,锥角为ψ,斜距为Ri。雷达以脉冲重复频率fr(Pulse Repetition Frequency,PRF)发射K个相干脉冲,信号波长为λ。雷达接收脉冲串并相关处理接收数据的时间称为相干处理间隔(Coherent Processing Interval, CPI)。
假设雷达和地面散射体之间的角度在CPI内是不变的。接收信号经过解调和匹配滤波后,第n个阵元接收到的散射体的回波信号与第一个阵元的相位差为
Δφ1=j (n-1)dcos φcos θ,n=1,2,…,N
由于与载机的相对运动,散射体同一阵元不同脉冲回波信号之间由多普勒频率产生的相移为
Δφ2=j2π(m-1) ,m=1,…,M
则位于(φk,θi)的杂波散射点的采样可以用下式表示为
$\begin{array}{c}c\left(\varphi_{k}, \theta_{i}\right)=\alpha_{i k} \exp \left(j \frac { 4 \pi V } { \lambda f _ { r } } \left[(m-1) \cos \left(\varphi_{k}+\alpha\right) \cos \theta_{i}+\right.\right. \\\left.\left.\frac{f_{r} d}{2 V}(n-1) \cos \varphi_{k} \cos \theta_{i}\right]\right) \\m=1, \cdots, M ; n=1, \cdots, N\end{array}$
式中,αik表示杂波块的幅度,与功率的关系式为
E =σ2ξik
式中,ξik为该散射单元的杂噪比(CNR),σ2为噪声功率。
将单个距离环上的杂波分成Nc块,则杂波块有效雷达截面积为
σik=σ0(ϕk,θi)×Sc=σ0(ϕk,θi)RiΔϕΔRsec φi
其中,σ0(φk,θi)是对应杂波块的地面反射系数,Sc为杂波块面积,Ri为杂波块与雷达之间的斜距,Δϕ=2π/Nc为每个杂波块的方位角度范围,ΔR为雷达的距离分辨率,φi为杂波块的擦地角,如图2 所示。
根据雷达方程,可得位于(ϕk,θi)杂波块的杂噪比ξik为
ξik=
其中,Pt表示发射峰值功率,Tp为脉冲发射宽度,Gt(ϕk,θi)表示发射增益,gt(ϕk,θi)表示接收增益,N0为输入噪声功率,Ls为系统损失。
1.2 STAP杂波抑制
由上文中机载预警雷达杂波模型可知,其地杂波与空间角度和多普勒都相关,呈现空时二维耦合特性,传统PD处理无法抑制。而STAP是机载预警雷达进行杂波和干扰抑制、实现目标探测的有效手段[11]。
STAP的目的就是设计一组最佳权向量,然后对各个脉冲匹配滤波输出求和,而这组权向量设计的依据就是使得最终输出的SCNR最大化,如接收阵列为N个阵元且发射M个相干脉冲,则就是共NM个输出加权求和,如图3 所示。
其中,xn,m表示第n个阵元第m个脉冲匹配滤波输出,则雷达接收的空时数据为
X=
对于滤波器中的最优权值,可以解以下优化问题获得:
式中,RX=E(XXH)为NM×NM维空时协方差矩阵,S为期望目标信号的空时导向矢量:
$ \begin{array}{l}\boldsymbol{S}=\boldsymbol{s}_{s} \otimes s_{t} \\\boldsymbol{s}_{s}=\left[\begin{array}{llll}1 & e^{j w_{s}} & \cdots & e^{j(N-1) w_{s}}\end{array}\right]^{\mathrm{H}} \\\boldsymbol{s}_{t}=\left[\begin{array}{llll}1 & e^{j w_{t}} & \cdots & e^{j(M-1) w_{t}}\end{array}\right]^{\mathrm{H}}\end{array}$
式中,ws为空间归一化角频率,wt为时间归一化多普勒频率。
最优权矢量Wopt为
Wopt=μ S
式中,μ=1/SH S为归一化复常数。
2 基于精细化杂波仿真的认知杂波抑制技术
传统的杂波仿真通常都是基于平地或者光秃地球的假设,只能定性地用来辅助验证算法,不能逼真地模拟真实地形的杂波数据,无法为雷达提供准确的先验知识。如果使用不准确的先验知识,处理性能将会更恶化。
雷达杂波受雷达系统、地形遮挡和地表反射等因素的影响,因此必须依据真实的雷达系统参数、真实的数字高程图(DEM)和真实的地表覆盖图(LCLU)进行信号级的杂波反演,才能为空时自适应处理提供准确的均匀样本,改善杂波抑制性能[12]。
但DEM、LCLU等外部先验信息与雷达回波在数据类型和数据格式上有很大差别,必须先进行格式转换和坐标变换,在这些先验信息的基础上进行系统建模和环境建模,得到高逼真度信号级杂波反演数据,才能获得准确的均匀杂波样本[13]。因此我们提出了一种基于精细化杂波仿真的认知杂波抑制技术,其原理框图如图4 。
该方法的关键是获取精细化的杂波仿真数据。具体可分为六个步骤,仿真流程图如图5 所示。
1)网格划分:根据雷达照射区域、雷达分辨参数在雷达坐标系中进行网格划分,划分出最小散射单元。
在雷达照射区域内,把地表分成多个ΔR×Δθ的栅格单元(其中ΔR和Δθ分别是雷达的角度和距离分辨力)。每个单元的天线增益、多普勒频移、距离、入射角、杂波散射率为一常数。
确定栅格单元的方法如下:
①确定ΔR。在地表面的距离环按雷达距离分辨单元划分。若脉冲压缩后的脉冲宽度为τ,则距离分辨单元为ΔR= 。
②确定Δθ。整个距离环的俯仰角固定,方位角为在360°范围内变化。选取合适的方位角变化量Δθ,使在空间的单独杂波源基本不能作多普勒分辨。
2)坐标变换:将散射单元转换到大地坐标系中。
根据雷达的GPS和惯导信息,将散射单元从雷达坐标系转换到载机坐标系再到北东地坐标系惯性坐标系,再转到地心直角坐标系(ECEF),最后到大地坐标系(经纬高)。
3)DEM插值及散射系数计算:利用DEM信息对转换到大地坐标系的散射单元计算相应的高程值,并根据LCLU计算散射单元的散射系数。其具体方法如下:
①DEM插值:根据DEM信息库信息进行插值;如图6 所示,先判断散射单元P所处的经纬度网格,然后进行内插点归一化:
则内插P点的高程为
②散射系数计算:根据地表信息计算散射单元的散射系数。
根据地表信息进行分类,以平原、丘陵和高原三类为例,运用修正的Mochin模型计算散射系数:
σ0= + cot2β0exp[- ]
其中,θ为散射单元的擦地角,f为雷达载频,其他系数与地形分类相关,如表1 所示。
表1 修正Mochin模型不同地类的系数Tab.1 The modified Mochin model coefficients for different land types |
| 地类 | A | B | β0 | |
|---|---|---|---|---|
| 平原 | 0.004 0 | π/2 | 0.20 | 1 |
| 丘陵 | 0.012 6 | π/2 | 0.40 | 1 |
| 高山 | 0.040 0 | 1.24 | 0.50 | 1 |
4)遮挡计算:根据各散射单元的数字高程值,利用射线追踪法计算遮挡。
以雷达为中心的射线经过的散射单元,计算每个散射单元的入射线的俯仰角,对比当前杂波点和前面所有杂波点的入射线的俯仰角,确认遮挡系数矩阵,如果有一个角比当前杂波点的入射线的俯仰角大,则被遮挡,遮挡系数为0,否则就没有被遮挡,遮挡系数为1。示意图如图7 所示。
5)杂波功率计算:根据雷达方程计算各散射点的杂波功率。
Pc(ϕ,θ)=
其中,Pt为雷达发射的峰值功率,G(ϕ,θ)为天线在(ϕ,θ)处的增益, l为雷达工作波长,σc为杂波的截面积,Lc为雷达系统对杂波的损耗,R为雷达到杂波处的距离。
6)信号级杂波回波仿真:模拟真实雷达系统的发射和接收过程,对杂波进行信号级仿真。
按照真实雷达参数模拟雷达发射和接收链路,接收到的杂波回波进行脉冲压缩和相参积累处理,获得全距离段的杂波样本数据。
通过以上步骤进行精细化杂波仿真,在获得全距离段的杂波仿真数据后,根据对应的距离段,利用距离样本计算先验协方差矩阵如式(14)所示:
Rc= Xl
其中,Xl表示第l个距离门的空时快拍,L表示快拍样本总数,(·)H表示向量的共轭转置。
然后将先验协方差矩阵与当前采样协方差矩阵融合,进行知识辅助空时自适应处理(KA-STAP)[14]:
=αR0+(1-α)Rc
其中,矩阵R0为由训练数据计算的协方差矩阵,Rc为由仿真数据得到的先验协方差矩阵,α∈ 由下式(16)-(17)确定。
α=
ρ= ‖Xl‖4- ‖Rc‖2
3 仿真性能分析
为了验证算法的性能,按照表2 中的参数进行了仿真:
表2 机载预警雷达及环境参数表Tab.2 The parameters of airborne early warning radar and environment |
| 参数 | 数值 |
|---|---|
| 载机高度 | 8 000 m |
| 载机速度 | 100 m/s |
| 载机经纬度 | (107,39) |
| 脉冲重复频率 | 2 500 Hz |
| 阵元个数 | 8 |
| 脉冲个数 | 128 |
| 雷达信号波长 | 0.6 m |
| 单元间距 | 0.3 m |
| 波束俯仰角 | 0° |
| 天线阵型 | 正侧视 |
| 目标距离门 | 600 |
| 目标多普勒门 | 30和52 |
按照上文的流程,利用DEM和LCLU等信息对杂波散射点的后向散射系数(NRCS)进行仿真,如图8 和图9 所示。
仿真结果可以反映平地NRCS普遍低,山地NRCS普遍高,山后被遮挡区域NRCS为0,与实际情况符合。
分别对仿真的信号级回波数据进行了传统STAP处理和利用仿真杂波样本辅助的KA-STAP处理,对比处理谱如图10 和图11 所示。
提取上面两图的第600个距离门剖面,得到两种方法的目标信杂噪比对比结果,如图12 所示。
在图12 中,对于位于杂波区的第52多普勒门的目标信杂噪比改善2 dB,另一位于清晰区的第30多普勒门的目标信噪比基本不变。结果证明了所提出方法对非均匀杂波区的目标性能有较大改善,且对其他目标性能无损失。
4 结束语
机载预警雷达面临日益复杂的战场环境,非均匀杂波抑制成为瓶颈难题,本文将精细化杂波仿真与认知处理相结合,提升了复杂杂波环境下的目标检测能力。
然而精细化的杂波仿真的耗时较长,对于基于数据流的雷达实时处理不利,未来可以研究结合载机平台航路规划和预测,先行调度杂波仿真,实现KA-STAP的实时化。