中国科技核心期刊      中国指挥与控制学会会刊     军事装备类重点期刊
指挥控制与仿真

指挥控制与仿真 >

2024 , Vol. 46 >Issue 4: 60 - 65

DOI: https://doi.org/10.3969/j.issn.1673-3819.2024.04.008

武器与信息系统

基于松弛变量法的目标散布区计算方法

  • 魏海光
展开
  • 江苏自动化研究所, 江苏 连云港 222061

魏海光(1979—),男,硕士,高级工程师,研究方向为舰艇电子信息系统。

收稿日期: 2023-06-11

  修回日期: 2023-06-26

  网络出版日期: 2024-07-29

收起

Calculation method of target distribution area based on relaxation variable method

  • WEI Haiguang
Expand
  • Jiangsu Automation Research Institute, Lianyungang 222061, China

Received date: 2023-06-11

  Revised date: 2023-06-26

  Online published: 2024-07-29

Fold

摘要

计算目标散布区大小是反舰导弹战术决策和目标捕获概率计算的前提条件,在研究反舰导弹对目标追击捕获模型的基础上,基于松弛变量法,建立了目标散布区计算方程,并给出了充要条件证明,获得了目标散布区的解析模型,在目标运动方向任意机动的假设下,得到了目标机动不受限条件下运动方向的最优值,给出了一般条件下的计算公式,通过仿真算例,对比了不同仿真参数条件下散布区域的变化情况,可为作战指挥人员决策使用提供直观参考和估算依据。

关键词： 松弛变量法; 散布区域; 目标捕获

本文引用格式

魏海光 . 基于松弛变量法的目标散布区计算方法[J]. 指挥控制与仿真, 2024 , 46(4) : 60 -65 . DOI: 10.3969/j.issn.1673-3819.2024.04.008

Abstract

The calculation of target distribution area is a prerequisite for anti-ship missile tactical decision-making and target acquisition probability calculation. On the basis of studying the target pursuit model of anti-ship missile, based on the relaxation variable method, the calculation equation for the target distribution is established, sufficient and necessary conditions are proved, the analytical model of target distribution area is obtained. Under the assumption that the target movement direction is arbitrary, and the calculation form under general conditions is given. Through the simulation example, the variation of distribution area under different conditions is compared, which can provide intuitive reference and estimation basis for the decision-making and use of the battle commanders.

Key words： relaxation variable method; distribution area; target acquisition

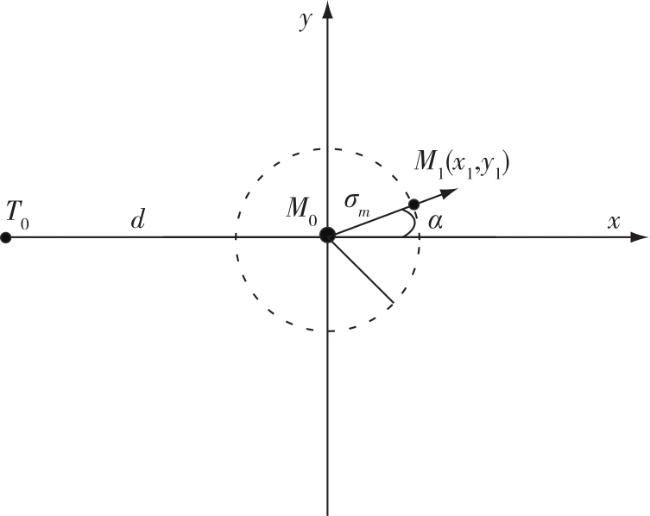
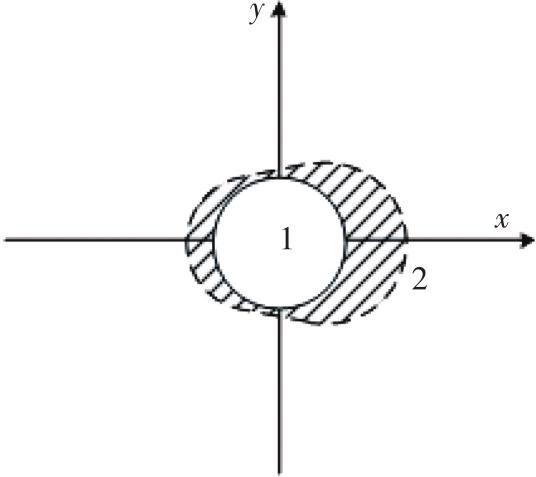
在反舰导弹对敌水面舰艇打击的作战行动中,命中目标的前提在于捕捉到目标,分析影响捕捉的因素时,快速计算或评估目标散布区域十分有意义。由于目标指示信息存在误差,目标机动存在不确定性,以及上述时间的误差积累等因素,目标的可能位置必然是一个更大的散布区域[1]。
侯学隆等[2]在目标以确定速度和未知方向机动散布条件下,推导了目标落入正方形和圆形散布区概率的优化计算方法;曾家有等[3]将平台定位、自控终点散布、目标指示、目标机动等误差因素纳入目标散布区的计算中,建立了捕捉概率计算模型;刘骁等[4]从统计概率角度估计目标散布,得到了末制导目标截获概率;董受全等[5]从超视距目标指示方法和精度出发,探讨了目标散布区域的一种形成方法,研究了目标散布区的确定方法;张邦钰等[6]选取矩形法和积分法与改进模型进行对比,对目标散布区域进行了估计;许俊飞等[7]未将散布误差的变化考虑进去,计算的捕获概率偏大;侯学隆等[8]基于条件概率密度方法,建立了CND-CS-ACND 散布概率密度模型;张海峰等[9]在研究目标散布误差时,仅考虑了时间因素;王宗杰等[10]基于蒙特卡洛法计算了水面舰艇目标散布圆;董斐等[11] 在构建搜捕模型时,仅使用一个确定的散布圆作为模型的输入,方法欠缺一定的实用性;于雪泳等[12]在求解目标位置散布概率密度时,利用泰勒公式将目标位置计算公式进行了简化处理。以上目标散布区计算方法,需要查询正态分布表或进行大量的仿真计算,使用复杂,无法直接获得关于目标位置散布的解析值,直观性差。
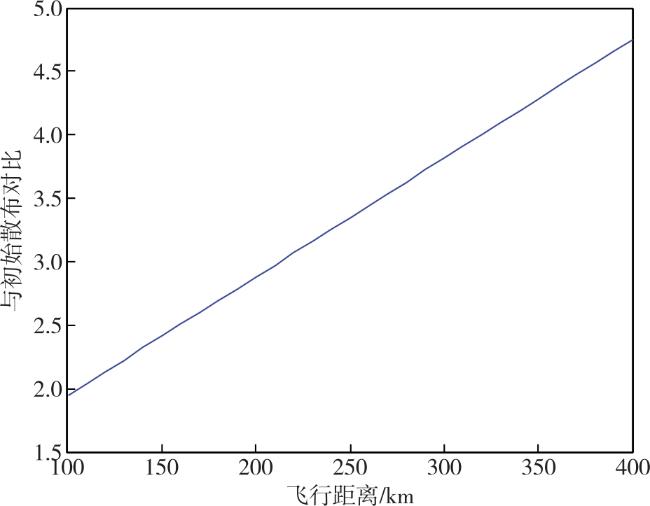
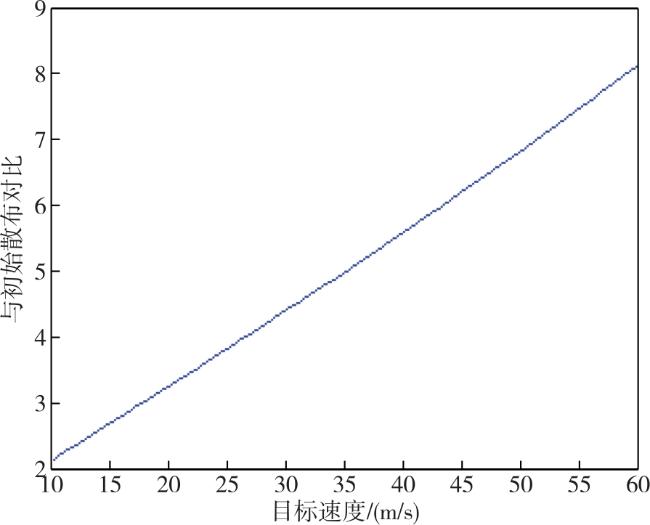
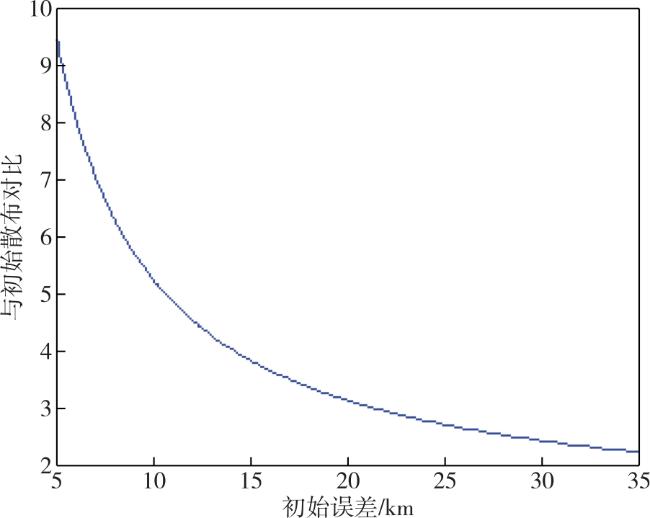
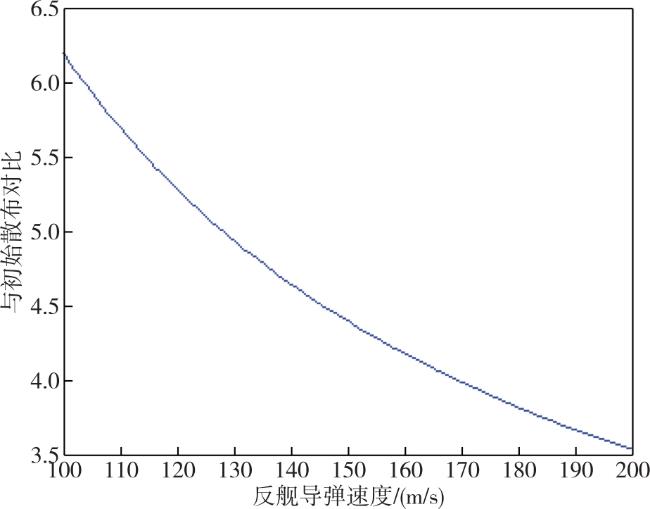
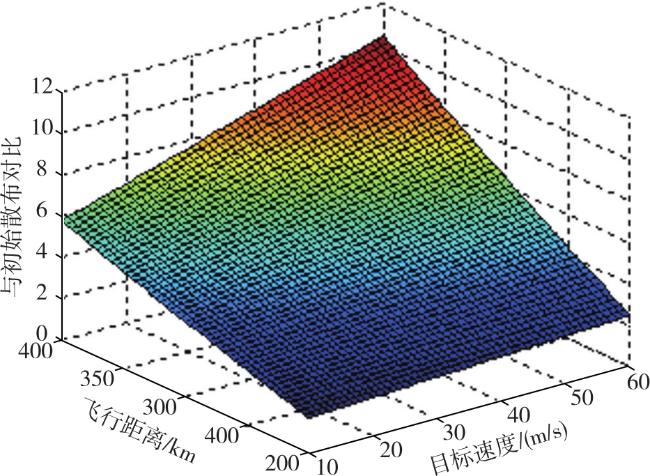
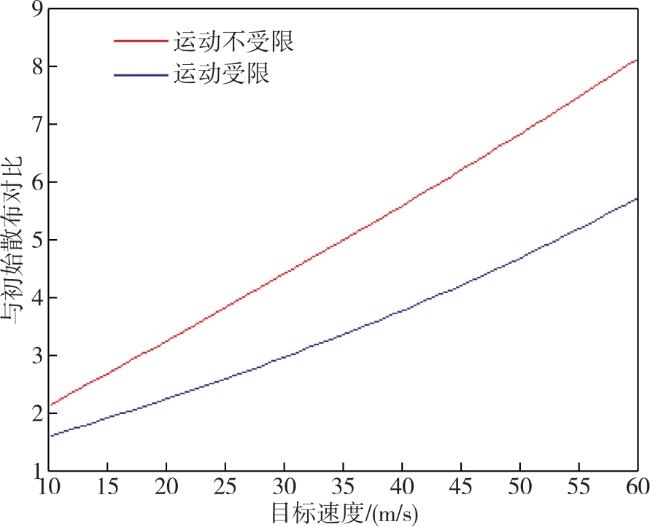
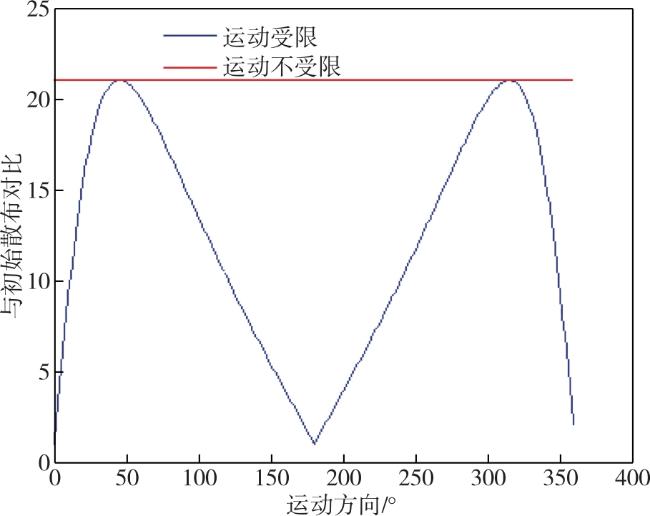
本文提出一种基于松弛变量法的目标位置散布区域解析计算方法,综合考虑目标初始误差、目标机动等因素,计算目标位置散布大小,仿真结果表明,该方法可快速计算目标误差散布区数值,具有一定应用价值。

1 问题描述

1.1 攻击态势设计

令发射平台与目标的距离为d0,目标的中心位置为M0,目标初始位置散布区域为以M0为圆心,半径为σ0的圆形;反舰导弹采用现在点射击方式,根据鲁棒性原则,假定目标在散布区内做任意方向机动。采用航路规划后,最终得到的导弹飞行航程将增大至d,以此建立敌我态势图如图1所示。图1中以目标中心M0为坐标原点,以导弹飞行方向为x轴,x轴垂线为y轴,建立笛卡尔坐标系。易知,反舰导弹航路机动不影响散布区域的计算,因此,可以将发射舰艇与目标之间的距离等效为长度为d的直线。
图1 初始态势图

Fig.1 Initial situation

1.2 问题求解方式转换

反舰导弹到初始散布圆近距离边缘和远距离边缘飞行时间不等,最终的目标散布区域呈梨形,如图2所示。由于梨形可能域的描述非常困难,因此,计算目标位置散布区半径的极大值,可以转化为计算散布区纵坐标y的最大值,以目标初始位置为中心,该最大值为半径的圆形区域将确保目标位于其中,虽然这会将目标散布区域变大,但结合反舰导弹末制导搜捕方式的设计[9],散布区的增大可以通过搜捕方式弥补。
图2 目标散布区变化图

Fig.2 Change of target distribution area

2 问题解析方程建立

针对图1中目标散布区域内位于第一象限内任一点A(x1,y1),从初始时刻开始,建立目标位置要素随时间变化方程和反舰导弹运动方程分别如式(1)和(2)所示。
x m = x 1 + v m t c o s α y m = y 1 + v m t s i n α
x d = - d + v d t y d = 0
式(1)(2)中,t为目标和反舰导弹的运动时间,vm为目标运动速度,α为目标运动方向,定义以x轴为其初始方向,逆时针增大,xm、ym为目标在t时刻位置的横坐标和纵坐标,vd为导弹飞行速度,(xd,yd)为反舰导弹在t时刻位置的坐标。由于A(x1,y1)在目标初始散布区域内,有
x 1 2+ y 1 2≤ σ 0 2
当导弹追击捕获到目标时,目标位置散布区半径取得最大值,后续导弹将转入对目标的跟踪打击阶段,可以认为已完成对目标的捕获,散布半径的继续增大对于目标捕获已经没有意义。此时满足:
xd=xm
将式(1)(2)(4)联立,消去其中的t和xm,为方便记,将ym替换为常用变量y,得到综合追击方程:
y=y1+ x 1 + d v d - v m c o s αvmsin α

3 问题转化

由式(5),前述计算散布区半径极值问题,可进一步分解为两个独立的极值问题求解,一是目标机动不受限条件下运动方向α的最优值求解,即对初始散布区内任意一点,目标以最大速度按何种方向运动,才能使式(5)取得最大值;二是在式(3)约束条件下,计算式(5)的极大值问题。由于松弛变量法可以通过引入非负的松弛变量,将约束条件为不等式的线性规划问题,转化为等式,便于极值问题计算。本文的问题满足约束条件为不等式的条件极值问题的特征[13],对约束条件式(3)引入一非负的松弛函数S1= x 2 2,将约束条件变为
φ1= x 1 2+ y 1 2- σ 0 2+S1=0
将问题转化为在约束条件(6)下,计算式(5)中y的最大值问题。

3.1 目标机动不受限条件下运动方向的最优值求解

对于式(5),令y=f(α)=y1+ x 1 + d v d - v m c o s αvmsin α,对其按α求导,得到
$f^{\prime}(\alpha)=v_{m}\left(x_{1}+d\right) \frac{\cos \alpha\left(v_{d}-v_{m} \cos \alpha\right)-v \sin \alpha \sin \alpha}{\left(v_{d}-v_{m} \cos \alpha\right)^{2}}$
即
$f^{\prime}(\alpha)=\frac{v_{m}\left(x_{1}+d\right)\left(v_{d} \cos \alpha-v_{m}\right)}{\left(v_{d}-v_{m} \cos \alpha\right)^{2}}$
根据单变量函数极值存在的必要条件[13]可知,当式(8)为0时,α0需满足:
vdcos α0-vm=0
从而得到
α0=arccos( v m v d)
在图1中态势及角度定义可知:0≤α≤90°。根据单变量函数极值存在充分条件的第一法则,当α<α0时,f'(α)>0;当α>α0时,f'(α)<0,因此α0为散布区半径取得最大值时的运动方向。由式(10)可知,α0仅与导弹速度、目标运动速度有关。

3.2 目标初始位置受限条件下的散布极值存在的必要性计算

目标函数为
Y=y1+ x 1 + d v d - v m c o s   α 0vmsin α0
根据拉格朗日乘数法[13],引入修正函数
F=Y-Pφ1=y1+ x 1 + d v d - v m c o s   α 0vmsin α 0-P( x 1 2+ y 1 2- σ 0 2+ x 2 2)
式(11)中,P是待定常数,分别计算F对x1、y1、x2的偏导数,以及极值存在的必要性条件,得到:
∂ F ∂ x 1 = c o t   α 0 - 2 P x 1 = 0 ∂ F ∂ y 1 = 1 - 2 P y 1 = 0 ∂ F ∂ x 2 = - 2 P x 2 = 0
由式(6)及(12),计算可得待定常数P和稳定点(x1,y1,x2)分别为:
P = 1 2 σ 0 s i n   α 0 x 1 = σ 0 · c o s   α 0 y 1 = σ 0 · s i n   α 0 x 2 = 0
P = - 1 2 σ 0 s i n   α 0 x 1 = - σ 0 · c o s   α 0 y 1 = - σ 0 · s i n   α 0 x 2 = 0

3.3 目标初始位置受限条件下散布极值存在的充分性证明

根据多元变量函数极值存在的充分条件[13],对于三元函数(11)极值存在的充分条件,在于判断式(15)(16)和(17)三个行列式的正负情况。
D1= ∂ 2 F ∂ x 1
D2= ∂ 2 F ∂ x 1 ∂ 2 F ∂ x 1 ∂ y 1 ∂ 2 F ∂ y 1 ∂ x 1 ∂ 2 F ∂ y 1
D3= ∂ 2 F ∂ x 1 2 ∂ 2 F ∂ x 1 ∂ y 1 ∂ 2 F ∂ x 1 ∂ x 2 ∂ 2 F ∂ y 1 ∂ x 1 ∂ 2 F ∂ y 1 2 ∂ 2 F ∂ y 1 ∂ x 2 ∂ 2 F ∂ x 2 ∂ x 1 ∂ 2 F ∂ x 2 ∂ y 1 ∂ 2 F ∂ x 2 2
对式(11),其行列式分别为
D 1 = - 2 P D 2 = 4 P 2 D 3 = - 8 P 3
当结果取值为(13)时,式(18)的结果为
D 1 = - 2 P = - 1 σ 0 s i n α 0 < 0 D 2 = 4 P 2 = 1 σ 0 2 s i n 2 α 0 > 0 D 3 = - 8 P 3 = - 1 σ 0 3 s i n 3 α 0 < 0
当结果取值为(14)时,式(18)的结果为
D 1 = - 2 P = 1 σ 0 s i n α 0 > 0 D 2 = 4 P 2 = 1 σ 0 2 s i n 2 α 0 > 0 D 3 = - 8 P 3 = 1 σ 0 3 s i n 3 α 0 > 0
根据函数极值存在的充分条件判断规则可知,当D2>0,D1<0,D3<0时,稳定点为极大值点;当所有行列式都是正的,如式(20)所示,稳定点为极小值点。因此式(13)为极大值,式(14)为极小值。
由式(13)(11),得到目标散布区半径最大值:
ymax=σ0 v d v d 2 - v m 2+d v m v d 2 - v m 2
从式(21)可知,散布区半径最大值与初始散布区大小、导弹飞行距离、导弹平均飞行速度、目标机动速度有关,与其他要素无关。
式(14)为对应的目标函数极小值只具有数学意义,不具有参考价值。

4 目标运动方向受限条件下散布区极值计算

以上问题讨论的一个前提条件是,目标可在散布区内向任意方向运动。在实际的作战过程中,还存在以下两种情况需要考虑:一是目标的运动方向受限,导弹的末端攻击方向受限;二是目标的运动方向受限,导弹的末端攻击方向不受限。此时的散布区最大值将会不同。

4.1 目标的运动方向受限,导弹的末端攻击方向受限

假设依靠其他方式可获知目标运动方向及其误差范围,转换为如式(22)所示:
α1≤α≤α2
式中,α1、α2分别为目标运动方向的下边界和上边界。
假设由于某些限制,反舰导弹末端的攻击方向固定,当α0<α1时,根据余弦函数的性质,此时目标运动方向应为α1,式(21)为
ymax=σ0 1 + ( v m s i n   α 1 v d - v m c o s   α 1 ) 2+ d · v m s i n   α 1 v d - v m c o s   α 1
当α2<α0<90°时,此时目标运动方向应为α2,式(21)为
ymax=σ0 1 + ( v m s i n   α 2 v d - v m c o s   α 2 ) 2+ d · v m s i n   α 2 v d - v m c o s   α 2
其他情况类似,需要注意α1、α2与α0之间的关系,最后计算得到的关系式与式(23)相同。

4.2 目标的运动方向受限,导弹的末端攻击方向不受限

在这种情况下,可以通过调整反舰导弹的末端攻击方式向,使式(23)取值最小,通常将攻击方向设置为- α 1 + α 2 2。

5 仿真分析

由于因导弹惯导设备引起的目标散布与导弹飞行距离成正比,在仿真时不考虑其影响。设置仿真初始态势条件如下:σ0为15 km,vm为25 m/s,飞行距离d为300 km,vd为180 m/s。为了对比明显,以下仿真图中的纵坐标为散布半径极值与初始散布误差半径比值。
当其他条件不变,反舰导弹飞行距离与散布对比之间的变化关系仿真如图3所示,目标速度与散布对比之间的变化关系仿真如图4所示,初始误差变化与散布对比之间的变化关系仿真如图5所示,反舰导弹速度与散布对比之间的变化关系仿真如图6所示,导弹飞行距离和目标速度同时变化条件下与散布对比之间的变化关系仿真如图7所示。
图3 反舰导弹飞行距离变化条件仿真图

Fig.3 Simulation diagram under change of flight distance

图4 目标运动速度变化条件仿真图

Fig.4 Simulation diagram under change of target speed

图5 初始误差变化条件仿真图

Fig.5 Simulation diagram under change of initial error

图6 反舰导弹速度变化条件仿真图

Fig.6 Simulation diagram under change of anti-ship missile flight speed

图7 目标速度和飞行距离同时变化条件仿真图

Fig.7 Simulation diagram under simultaneous change of flight distance and target speed

由图3可知,当飞行距离约213 km时,散布区将扩大为初始的三倍;由图4可知,当目标的运动速度约为35.1 m/s时,散布区将扩大为初始的五倍;由图5可知,当初始散布约为14 km时,散布区最终扩大为初始的四倍;由图6可知,当反舰导弹的平均速度约为140 m/s时,散布区最终扩大为初始的四倍;由图7可知,在目标散布确定时,可以调节距离和目标的速度间组合,确定合适的攻击方案。
在目标的速度在10~60 m/s范围内,当目标的运动方向受限在某个区间(图中运动方向设置为30°)时,与运动方向完全不受限的对比图如图8所示;当目标速度为25 m/s,目标的运动方向受限在0~359°之间时,与运动方向完全不受限的对比如图9所示。
图8 目标速度方向为30°与方向不受限的散布对比图

Fig.8 Comparison between limited in 30° and unlimited target speed direction

图9 目标速度方向受限与不受限间对比图

Fig.9 Comparison between limited and unlimited target speed direction

由图8可以发现,当补充了关于目标的额外信息(运动方向)后,目标的散布区将大大缩小;由图9可以发现,运动不受限是所有情况中最差的情况,如果满足该条件,那么计算出的散布区半径将肯定大于其他条件下的散布区半径。

6 结束语

通过定量计算目标位置散布区最大值,可以为战术决策提供一种具有鲁棒性的控制输入,保证在最差条件下对目标的有效攻击,对提高反舰导弹的作战效能有一定的军事意义。本文基于松弛变量法,在目标初始散布为圆形的前提下,获得目标位置散布区在特殊条件和一般条件下极值的解析表达式,在实际使用时,还需增加由于惯导漂移引起的与导弹飞行距离成正比的误差。后续将在目标初始位置散布为更具有代表性的椭圆的条件下,计算散布区的解析形式,为目标打击决策提供更具有普遍意义的参考。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
景永春, 谢春思, 熊正祥, 等. 基于目标散布的反舰导弹捕捉概率研究[J]. 战术导弹技术, 2016(4): 48-52.

JING YC, XIE C S, XIONG Z X, et al. Study of acquiring probability of anti-ship missile based on target diffusion[J]. Tactical Missile Technology, 2016(4): 48-52.

[2]
侯学隆, 姜青山. 海上机动目标CND-CS-UC散布规律研究[J]. 指挥控制与仿真, 2017, 39(4): 40-45, 59.

DOI

HOU X L, JIANG Q S. Research on the CND-CS-UC distribution rules of marine moving target[J]. Command Control & Simulation, 2017, 39(4): 40-45, 59.

[3]
曾家有. 各种因素对现在点射击方式反舰导弹捕捉概率的影响分析[J]. 兵工学报, 2011, 32(6): 719-724.

ZENG J Y. Influenceanalysis of various factors to acquiring probability of anti-ship missile with shooting at target’s immediate position[J]. Acta Armamentarii, 2011, 32(6): 719-724.

[4]
刘骁, 唐胜景, 朱大林, 等. 制导弹药末段目标截获概率研究[J]. 兵工学报, 2015, 36(2): 287-293.

DOI

LIU X, TANG S J, ZHU D L, et al. Research on target acquisition probability in the terminal guidance of guided munition[J]. Acta Armamentarii, 2015, 36(2): 287-293.

DOI

[5]
董受全, 刘志强. 超视距目标指示与目标散布区域的研究[J]. 飞航导弹, 2000(10): 39-41.

DONG S Q, LIU Z Q. Research on over the horizon target indication and target dispersion area[J]. Aerodynamic Missile Journal, 2000(10):39-41.

[6]
张邦钰, 沈培志. 一种反舰导弹目标捕捉概率计算模型的改进[J]. 四川兵工学报, 2015, 36(3): 20-22, 59.

ZHANG B Y, SHEN P Z. Improving of an anti-ship missile acquiring probability calculation model[J]. Journal of Sichuan Ordnance, 2015, 36(3): 20-22, 59.

[7]
许俊飞, 卢发兴, 王航宇, 等. 多误差影响下的末制导炮弹捕捉概率建模方法[J]. 海军工程大学学报, 2021, 33(1): 107-112.

XU J F, LU F X, WANG H Y, et al. Modeling method for capturing probability of terminal guided projectile under influence of multiple errors[J]. Journal of Naval University of Engineering, 2021, 33(1): 107-112.

[8]
侯学隆, 王宗杰, 姜青山. 海上机动目标正态概略航向下的位置散布规律研究[J]. 指挥控制与仿真, 2018, 40(6): 53-59.

DOI

HOU X L, WANG Z J, JIANG Q S. Research on the Position distribution of marine moving target on approximate course under normal distribution[J]. Command Control & Simulation, 2018, 40(6): 53-59.

[9]
张海峰, 于忠琳, 谢宇鹏. 基于方向协同的反舰导弹捕捉概率研究[J]. 指挥控制与仿真, 2020, 42(6): 47-51.

DOI

ZHANG H F, YUZ L, XIE Y P. Probability of capture of anti-ship missiles based on direction coordination[J]. Command Control & Simulation, 2020, 42(6): 47-51.

[10]
王宗杰, 罗木生, 侯学隆. 基于蒙特卡洛法的目标散布圆特征计算模型研究[J]. 弹箭与制导学报, 2019, 39(2): 147-151.

WANG Z J, LUO M S, HOU X L. A study on the calculation model of target dispersion circle based on Monte Carlo method[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2019, 39(2): 147-151.

[11]
董斐, 刘文彪, 欧阳中辉, 等. 反舰导弹末制导雷达搜捕方式确定模型[J]. 现代防御技术, 2019, 47(4): 30-37.

DONG F, LIU W B, OUYANG Z H, et al. Determination model of terminal guidance radar’s catching mode for antiship missile[J]. Modern Defence Technology, 2019, 47(4): 30-37.

[12]
于雪泳, 李长军, 黄文斌. 引导兵力通报情况下水面目标位置散布分析[J]. 舰船科学技术, 2013, 35(5): 119-122.

YU X Y, LIC J, HUANG W B. Research on probability density of object location when information is received from spy platform[J]. Ship Science and Technology, 2013, 35(5): 119-122.

[13]
《数学手册》编写组. 数学手册[M]. 北京: 高等教育出版社,2004:232-238.

《Mathematical Handbook》WritingGroup. Mathematical Handbook[M]. BEIJING: Higher Education Press,2004:232-238.

Options
文章导航

/

〈 〉