基于BWM的反坦克分队打击目标模糊优选

尹星; 权力

doi:10.3969/j.issn.1673-3819.2021.02.014

指挥控制与仿真 >

2021 , Vol. 43 >Issue 2: 76 - 81

DOI: https://doi.org/10.3969/j.issn.1673-3819.2021.02.014

理论研究

基于BWM的反坦克分队打击目标模糊优选

尹星 ¹ ,
权力 ²

展开

1.陆军指挥学院, 江苏南京 210045
2.陆军信息保障室, 北京 100042

作者简介：尹星(1988—),男,江苏连云港人,硕士,讲师,研究方向为作战模拟与仿真。

权力(1987—),男,硕士,工程师。

Copy editor: 张培培

收稿日期: 2020-11-26

修回日期: 2020-12-24

网络出版日期: 2022-04-29

收起

Fuzzy Optimization of Antitank Element Attacking Target Based on Best-Worst Method

YIN Xing ¹ ,
QUAN Li ²

Expand

1. Army Command College, Nanjing 210045
2. Army Information Guarantee Office, Beijing 100042, China

Received date: 2020-11-26

Revised date: 2020-12-24

Online published: 2022-04-29

Fold

摘要

在借鉴以往打击目标评估指标研究的基础上,结合反坦克分队任务特点,提出了4方面共15项目标评估指标体系;使用最优最差法,计算目标评估指标的权重;采用模糊优选方法,通过规范化处理得到目标评估指标值,并结合指标权重对反坦克分队打击目标价值进行综合排序。最后,基于某实例想定,对反坦克分队打击目标排序问题进行分析,验证了上述方法的有效性和可实施性,能够为反坦克分队指挥员在火力打击活动中优化目标打击排序提供决策依据。

关键词： 反坦克分队; 评估指标; 最优最差法; 模糊优选

本文引用格式

尹星 , 权力 . 基于BWM的反坦克分队打击目标模糊优选[J]. 指挥控制与仿真, 2021 , 43(2) : 76 -81 . DOI: 10.3969/j.issn.1673-3819.2021.02.014

Abstract

On the basis of the previous research of the evaluation indexes of attacking targets, according to the special mission features of antitank element, this paper proposes the evaluation index system of attacking targets, which includes four aspects and fifteen indexes; uses BWM to calculate the weight of the evaluation of index; adopts a fuzzy optimization method, calculates the results of indexes through normalization, and calculates the value of attacking targets according to index weight. At last, based on the experiment scenario,this paper analyzes the problem of attacking target compositor,which verifies the validity of the above-mentioned method and provides decision-making evidence for commander of antitank element to sort the attacking targets in the process of fire strike.

Key words： antitank element; evaluation index; best-worst method; fuzzy optimization

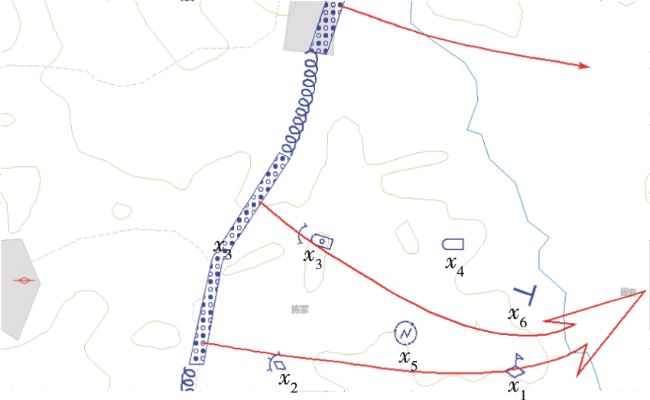
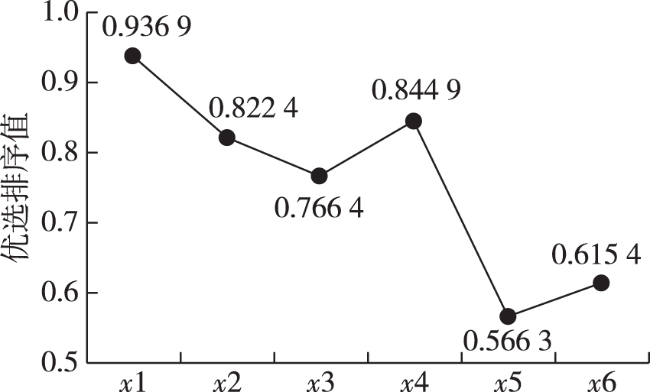
随着新型陆军的建设发展,反坦克分队作为反装甲作战的重要力量,在远、中、近反坦克火力配系中越来越关键,在未来的战斗中将发挥更大的作用^[1]。作为反坦克分队指挥员,如何根据敌方不同的装甲武器以及实际战场环境等因素,合理选择打击目标,是提升反坦克火力作战效能以及优化作战运用首先要解决的问题。然而,随着信息化智能化战争的发展,战场态势瞬息万变,战场目标的动态性、多样性也随之加强,造成反坦克分队打击目标的优化选择愈来愈复杂。因此,亟须依据反坦克分队任务特点,科学制定打击目标评估指标体系,研究打击目标综合排序方法,为反坦克分队指挥员在火力打击活动中优化目标排序提供决策依据。

对于目标排序问题,目前也有很多的研究,主要思路是建立评估指标体系,通过计算指标权重的方法进行排序,算法主要包括多属性效用理论(UTA方法^[2]、层次分析法(AHP)^[3]、灰色关联分析法^[4]等)、非经典方法(基于优势粗糙集的方法^[5]、鲁棒有序回归方法^[6]等)、基于级别优先关系的方法(ELECTRE方法^[7]、PROMETHEE方法^[8]等)等。此外,在反坦克分队选择打击目标方面也有一定的应用研究,周新初^[9]等学者根据车载反坦克导弹的作战运用特点,结合AHP理论建立了反坦克导弹火力分配的优化模型。刘晓雷^[10]等学者根据某型反坦克导弹系统,采用递归算法提出火力分配模型算法。连鲁军^[11]等学者运用人工鱼群算法,对反坦克火力分配问题进行了最优化求解。在这些方法中,由于AHP的简便性和易操作性,也应用到了目标排序问题中。另外,对于反坦克分队的研究主要集中于多目标火力分配方面。

Razaei^[12-13]指出了非结构化地进行两两比较会带来判断矩阵不一致的情况,为完善该情况,提出了最优最差法(BWM),首先,在待比较的对象中确定最优对象和最差对象,然后,将这两个对象和其他对象进行两两比较,得到两个比较向量,最后,得到所有对象的权重值。此外,运用AHP方法需要两两比较

n (n - 1) 2

次,而运用BWM方法只需要比较2n-3次,随着n值的变大,BWM比AHP方法需要的比较次数更少。

通过上述分析,本文在考虑反坦克分队任务特点的基础上,分析目标打击价值的影响因素,构建了反坦克分队打击目标的评估指标体系,提出了一种基于BWM的反坦克分队模糊优选方法,既可以减少两两比较的次数,得到更加一致的比较结果,提高权重的科学性,又通过模糊优选方法^[14-15],量化决策分析值,采用逼近于理想的排序方法,得到打击目标的综合排序值,能够辅助反坦克分队指挥员快速准确、比较合理地选择打击目标。

1 反坦克分队打击目标评估指标体系分析

反坦克分队选择打击目标,可以转换为怎样依据目标价值属性确定目标打击决策的问题。首先要考虑反坦克分队的基本作战任务,根据文献[1],其主要包括:1)击毁敌坦克、步兵战斗车辆等装甲目标;2)破坏敌其他地面重要的武器系统等;3)破坏敌工程设施和其他军事设施;4)必要时,与敌武装直升机做斗争。其次,衡量打击目标综合价值,必须要综合分析影响目标价值的各项因素;同时,也要保证目标价值分析的可操作性,需筛除一些重合或者模糊的指标。

因此,本文以突出重点和实际需要为准则,结合反坦克分队的任务特点,在比较以往各种价值指标体系的基础上^[16-17],构建了反坦克分队打击目标评估指标体系,主要包含任务一致性、毁伤有利性、打击迫切性和打击效用性等4个方面,以及各方面对应组成的15项综合评估指标,如图1所示。

显示原图|下载原图ZIP|生成PPT

图1 反坦克分队打击目标评估指标体系

2 反坦克分队打击目标价值排序模型与方法

2.1 基于BWM的主观权重计算模型

根据Razaei^[12-13]提出的最优最差法,可以得到基于BWM的主观权重计算模型,具体步骤如下。

Step1:定义指标集

在该步骤中,设影响反坦克分队打击目标价值的一级评估指标集合D={d₁,d₂,d₃,d₄},二级评估指标的集合C={c₁,c₂,...,c_n},n=15。

Step2:确定最优指标和最差指标

在一级评估指标集合D中,决策者需要确定最优(最重要)的指标,记为d_B;确定最差(最不重要)的指标,记为d_W。评价标度如表1所示。

表1 评价标度

标度	含义
1	两者同等重要
2	前者比后者略微重要
3	前者比后者比较重要
4	前者比后者中度重要
5	前者比后者明显重要
6	前者比后者非常重要
7	前者比后者特别重要
8	前者比后者极其重要
9	前者比后者极端重要

Step3:确定最优指标相对于其他指标的权重

根据表1,通过最优指标和其他指标相对重要度的两两比较,分别得到相应的标度,可表示为权重向量A_B,即

(1)A_B=(a_B₁,a_B₂,...,a_Bm)

式中,a_Bm表示d_B相对于第m个指标的权重。

Step4:确定其他指标相对于最差指标的权重

同样如表1所示,通过其他指标和最差指标相对重要度的两两比较,分别得到相应的标度,表示为权重向量A_W,即

(2)A_W=(a₁_W,a₂_W,...,a_mW)

式中,a_mW表示第m个指标相对于d_W的权重。

Step5:求解最优权重

通过线性模型,使得指标的最佳权重集合满足{|

w B d

-a_Bj

w j d

|,|

w j d

-a_jW

w W d

|}的最大绝对差最小化。其中,

w B d

表示最优指标B的权重,

w W d

表示最差指标W的权重,

w j d

表示第j个指标的权重,因此,也可以将该问题转化为求约束优化问题的最优解。

(3)

m i n m a x j {| w B d - a B j w j d |, | w j d - a j W w W d |} s . t . ∑ j w j d = 1 w j d ≥ 0

式(3)可以转化为约束优化问题,即

(4)

m i n ξ s . t . | w B d - a B j w j d | ≤ ξ | w j d - a j W w W d | ≤ ξ ∑ j w j d = 1 w j d ≥ 0

求解式(4),可以得到各评估指标的最优权重集合(

w 1 d *

w 2 d *

,...,

w m d *

)和ξ^*。ξ^*是表示求解权重结果的指示值,ξ^*值越接近于0,表明所求解的权重结果误差越小,也说明越可信。

Step6:求解集合C的最优权重

对于不同的一级评价指标d_i(i=1,2,3,4),分别重复步骤2~5,求出最优权重集合(

w 1 c *

w 2 c *

,...,

w n c *

)和ξ^*,并根据ξ^*的值判断权重结果是否可信。

最后,求得目标价值评价指标集C的最优权重W,公式如下:

(5)

$w i *$ = $w i c * × w 1 d * 1 ≤ i ≤ 3 w i c * × w 2 d * 4 ≤ i ≤ 8 w i c * × w 3 d * 9 ≤ i ≤ 11 w i c * × w 4 d * 12 ≤ i ≤ 15$

2.2 模糊优选理论与模型

20世纪60年代,美国控制论专家、加利福尼亚大学扎德教授创立了模糊数学^[14]。模糊数学可以将形式化思维(精确数学)的一系列成果,应用到各类复杂系统中,目前在数理、经济、军事等领域得到了广泛的应用。

1)目标属性值的规范化处理

设共有m个目标组成目标集合X={x₁,x₂,...x_m},则目标集X在目标评估指标集C下的决策矩阵为R=(r_ij)_m_×_n,式中,r_ij为目标x_i(1≤i≤m)在评估指标c_j(1≤j≤n)上的属性值。

通常情况下,r_ij的确定主要有以下方法。

①通过装备试验、部队实战化训练与演习、模拟仿真实验或实战等途径获得。

②通过专家的直觉、经验、统计、排序和推理,确定模糊隶属函数获得。模糊隶属大致有以下6种形态:

a) 线性隶属函数:u(x)=1-kx

b) Γ隶属函数:u(x)=exp(-kx)

c) 凹(凸)形隶属函数:u(x)=1-ax^k

d) 柯西隶属函数:u(x)=

1 (1 + k x 2)

e) 岭形隶属函数:

u(x)= $12$ - $12$ sin $π b - a x - b + a 2$

f) 正态隶属函数:u(x)=exp

- (x - a) 2 2 b 2

③利用价值中心法,通过确定目标x_i的属性值评价曲线获得。一般情况下,采用线性、凹性、凸性、凸/凹性和凹/凸性等标准函数形式对属性值进行评价。除此之外,也可根据实际情况定义其他形式的评价函数。

在计算目标综合价值前,必须要对指标的数值进行规范化处理,而指标一般包括定性指标和定量指标。对于定性指标,通常根据专家意见,将定性的评价值转化为确定的定量值,也可以采用模糊数或区间数的形式进行表示;对于定量指标,通常是建立相应的数学转换关系,将定量值转化为上下限分别是1和0的实数,这样可以实现对不同量纲的指标进行相互比较,从而获得综合排序值,其中,数学转换关系可以表示为函数F(x):R→[0,1]。

2)模糊优选模型

由前面可知,目标x_i在评估指标集C的决策矩阵为

$X i = (r i 1, r i 2, ..., r i n) i = 1,2, ..., m$ 。

定义系统的优向量为Y=(y₁,y₂,...,y_n)。

定义系统的劣向量为B=(b₁,b₂,...,b_n)。

目标x_i以隶属度u_i隶属于系统的优向量Y,则目标x_i以隶属度1-u_i隶属于系统的劣向量B。

定义系统的加权优距离(贴近度)为

(6)D(X_i,Y)=u_i

∑ j = 1 n (w j * | r i j - y j |) p 1 p

=u_i

∑ j = 1 n (w j * | r i j - 1 |) p 1 p

定义系统的加权劣距离(贴近度)为

(7)D(X_i,B)=(1-u_i)

∑ j = 1 n (w j * | r i j - b j |) p 1 p

=(1-u_i)

∑ j = 1 n (w j * r i j) p 1 p

因此,模糊优选模型可表示如下

(8)min F(u_i)=[D(X_i,Y)]²+[D(X_i,B)]²=

u i 2

∑ j = 1 n [w j * (1 - r i j)] p 2 p

+(1-u_i)²

∑ j = 1 n (w j * r i j) p 2 p

求解

d F (u i) d u i

=0,得到u_i的最优值计算模型,即目标x_i的重要性特征值为

(9)u_i=

1 1 + ∑ j = 1 n [w j * (1 - r i j)] p ∑ j = 1 n (w j * r i j) p 2 p

根据u_i(i=1,2,...,m)值的大小,就可以对目标x₁,x₂,...,x_m进行优选排序。其值越大,目标的优先级越高。

3 应用案例

本文以某合成分队开进展开与火力准备阶段中,对敌方前沿支撑点进行火力打击的军事行动为例^[16]。我方下属的某反坦克分队,已开进到敌防御前沿地域,支援我前沿攻击分队。敌左翼防御方是某连,于3天前进驻该地,已在敌前沿部署了雷场、铁丝网等,并依托地形构筑了工事,作为敌前沿防御支撑点。此时,反坦克分队通过整合自身和上级侦察情报,发现我火力范围内,有6个重要目标需要打击,详细部署如图2所示。其中,x₁为坦克指挥车,x₂为坦克,x₃为步战车,x₄为通信车,x₅为装甲输送车,x₆为迫击炮。

显示原图|下载原图ZIP|生成PPT

图2 敌兵力部署示意图

3.1 基于BWM计算打击目标价值属性权重

根据前面描述的内容,需要邀请专家首先按照流程,确定打击目标评估指标的权重。

Step1:确定属性集

我们在第一节中,已经确定了反坦克分队的打击目标评估指标体系,分为一级评价指标集和二级评价指标集,具体如表2所示。

表2 打击目标价值属性集

一级评价指标	二级评价指标
	与本级作战任务的一致性c₁
任务一致性d₁	与上级作战任务的一致性c₂
	与作战时节任务的一致性c₃
	目标的机动能力c₄
	目标的隐蔽程度c₅
毁伤有利性d₂	目标的防护程度c₆
	目标的外部形态c₇
	目标信息来源可靠性c₈
	目标的匹配程度c₉
对我威胁性d₃	目标的对抗程度c₁₀
	对我行动妨碍程度c₁₁
对敌有用性d₄	战场位置重要性c₁₂
	对敌体系结构影响性c₁₃
	目标可替代性c₁₄
	目标心理价值c₁₅

Step2:确定最优属性和最差属性

以对一级评价指标集D为例,确定该集合的最优属性和最差属性,经过综合分析讨论,最优属性为“任务一致性”,即d₁;最差属性为“毁伤有利性”,即d₂。

Step3:确定最优属性相对于其他属性的权重

根据“1-9”重要度评价标度,可以得到d₁相对于其他指标的权重向量A_B=(1,4,2,3)。

Step4:确定其他属性相对于最差属性的权重

根据“1-9”重要度评价标度,可以得到其他指标相对于d₂的权重向量A_W=(4,1,3,2)。

Step5:求解最优权重

根据公式(4),可以求出最优权重集合为(0.465 5, 0.103 5, 0.258 6, 0.172 4),此时ξ^*=0.051 7,表明所求解的值还是比较可信的。

Step6:求解二级评价指标的权重

不断重复上述的步骤2~5,分别求解出不同一级指标下所包含二级指标的权重,再根据公式(5),求得评价指标集的最优权重,具体如表3所示。

表3 打击目标价值属性权重值

一级指标	指标权重	二级指标	指标权重	综合权重
	0.465 5	c₁	0.291 7	0.135 8
d₁		c₂	0.541 6	0.252 1
		c₃	0.166 7	0.077 6
	0.103 5	c₄	0.147 1	0.015 2
		c₅	0.147 1	0.015 2
d₂		c₆	0.088 2	0.009 1
		c₇	0.397 0	0.041 1
		c₈	0.220 6	0.022 8
	0.258 6	c₉	0.541 6	0.140 1
d₃		c₁₀	0.166 7	0.043 1
		c₁₁	0.291 7	0.075 4
	0.172 4	c₁₂	0.258 6	0.044 6
d₄		c₁₃	0.465 5	0.080 3
		c₁₄	0.103 4	0.017 9
		c₁₅	0.172 4	0.029 7

3.2 基于模糊优选模型计算目标重要性特征值

通过上述分析,拟打击目标集合X={x₁,x₂,...,x₆}={坦克指挥车,坦克,步战车,通信车,迫击炮,装甲输送车},由于为定性指标,可建立从军事价值定性评价到区间数的规范化映射,如表4所示。

表4 定性指标的定量化赋值表

定性指标值	差	较差	一般	好	很好
	弱	较弱	一般	较强	强
	低	较低	一般	较弱	高
区间数	[0,0.2]	[0.2,0.4]	[0.4,0.6]	[0.6,0.8]	[0.8,1]

根据专家意见以及表4内容,通过规范化处理,6个目标在上述15个价值属性的值如表5所示。

表5 打击目标决策属性值

	x₁	x₂	x₃	x₄	x₅	x₆
c₁	0.8	0.7	0.6	0.8	0.5	0.5
c₂	0.8	0.6	0.6	0.9	0.6	0.5
c₃	0.8	0.7	0.6	0.8	0.6	0.6
c₄	0.6	0.6	0.5	0.7	0.9	0.5
c₅	0.4	0.7	0.7	0.3	0.4	0.5
c₆	0.5	0.5	0.6	0.8	0.8	0.7
c₇	0.7	0.7	0.8	0.5	0.6	0.7
c₈	0.7	0.9	0.8	0.6	0.6	0.7
c₉	0.9	0.9	0.8	0.6	0.3	0.7
c₁₀	0.8	0.8	0.7	0.2	0.7	0.5
c₁₁	0.8	0.7	0.7	0.2	0.8	0.5
c₁₂	0.8	0.7	0.7	0.8	0.7	0.6
c₁₃	0.8	0.5	0.5	0.8	0.4	0.3
c₁₄	0.7	0.5	0.5	0.8	0.6	0.5
c₁₅	0.8	0.5	0.5	0.8	0.7	0.4

根据公式(9),令p=1,可以算出各目标的优选排序值:坦克指挥车(0.936 9)、坦克(0.822 4)、步战车(0.766 4)、通信车(0.844 9)、迫击炮(0.615 4)、装甲输送车(0.571 3),具体如图3所示。

显示原图|下载原图ZIP|生成PPT

图3 拟打击目标优选排序值

根据算法得出的优选排序值的大小进行排序,可得到如下结果:x₁>x₄>x₂>x₃>x₆>x₅,即说明反坦克分队最优先打击的目标是坦克指挥车,然后依次是通信车、坦克、步战车、迫击炮、装甲输送车,该排序结果和实际作战进程比较相符,因为要考虑反坦克分队的任务特点,也要综合衡量拟打击目标的对敌体系重要程度以及对我威胁度等因素。因此,可以说明该方法是比较科学、合理的,能够为反坦克分队指挥员优化打击目标排序提供辅助决策支撑作用。

4 结束语

本文结合反坦克分队的任务特点,在借鉴以往打击目标评估指标研究的基础上,围绕任务一致性、毁伤有利性、打击迫切性和打击效用性等对目标影响较大的因素,提出了4方面共15项指标的综合评估指标体系;针对反坦克分队打击目标排序问题,提出了一种基于BWM的反坦克分队打击目标模糊优选方法,确定指标数值及权重,并计算目标的综合价值;最后,根据实例想定,对目标排序问题进行分析,实例分析结果表明本文所提方法的有效性和可实施性,为反坦克分队指挥员在火力打击活动中优化打击排序有参考价值。

下一步主要工作:一是针对现有BWM方法,进行改进完善,进一步提高权重计算的客观性;二是本文主要解决的是打击目标排序问题,而没有考虑如何将多个目标分配给多个反坦克武器,后面需要加强该方面的研究,进一步为反坦克分队指挥员优化打击效果提供决策支撑。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序

[1]	赵学, 马骏. 信息化条件下反坦克炮兵作战运用[M]. 沈阳: 白山出版社, 2008.

[2]	段雪妍, 余思勤, 范琛, 等. 基于UTA方法的多目标优化模型[J]. 数学的实践与认识, 2015, 45(23):138-146.

[3]	胡稳权, 王正新, 陈艺. 基于AHP与BWM方法的跨境电商零售进口税收新政实施风险评估[J]. 科技创业, 2018, 32(10):50-52.

[4]	杨宇飞, 刘建闯. 基于灰色关联分析法的炮兵火力打击目标排序问题研究[J]. 四川兵工学报, 2013, 34(3):61-63.

[5]	李佳, 梁吉业, 庞天杰. 一种基于优势粗糙集的多属性决策排序方法[J]. 南京大学学报(自然科学), 2016, 52(5): 844-852.

[6]	张宏军, 尹成祥, 綦秀利, 等. 多准则决策中的鲁棒有序回归方法综述[J]. 控制与决策, 2017, 32(5):769-779.

[7]	Govindan K, Jepsen M B. Electre: A Comprehensive Literature Review on Methodologies and Applications[J]. European Journal of Operational Research, 2016, 250(1):1-29. DOI

[8]	Behzadian M, Kazemzadeh R B, Albadvia, et al. Promethee: a Comprehensive Literature Review on Methodologies and Applications[J]. European Journal of Operational Research, 2010, 200(1):198-215. DOI

[9]	周新初, 张智智, 夏军, 等. 车载反坦克导弹火力分配优化模型[J]. 火力与指挥控制, 2011, 36(2):109-111,118.

[10]	刘晓雷, 孟婷婷, 斐文. 某型反坦克导弹多目标火力分配优化模型[J]. 火力与指挥控制, 2014, 39(增刊):34-36.

[11]	连鲁军, 吴士琦. 基于人工鱼群算法的反坦克火力分配模型研究[J]. 浙江树人大学学报, 2013, 13(1):6-10.

[12]	Rezaei J. Best-worst Multi-criteria Decision-making Method[J]. Omega, 2015(53):49-57.

[13]	Rezaei J. Best-worst Multi-criteria Decision-making Method:Some Properties and Alinear Model[J]. Omega, 2016(64):126-130.

[14]	罗小明, 等. 非对称作战数学建模与仿真分析[M]. 北京: 国防工业出版社, 2012.

[15]	霍晓飞, 武文军, 张现国. 多指标模糊优选方法在敌机主攻方向判断上的应用[J]. 射击学报, 2010(1):20-22.

[16]	朱浩浩, 陈勇, 陈铁健, 等. 合成分队目标综合排序方法研究[J]. 电光与控制, 2019, 26(5):95-99.

[17]	任富兴, 王雪琴. 联合火力战毁伤理论[M]. 北京: 解放军出版社, 2010.

Options

文章导航

模态框（Modal）标题

摘要

本文引用格式

Abstract

1 反坦克分队打击目标评估指标体系分析

图1 反坦克分队打击目标评估指标体系

2 反坦克分队打击目标价值排序模型与方法

2.1 基于BWM的主观权重计算模型

表1 评价标度

2.2 模糊优选理论与模型

3 应用案例

图2 敌兵力部署示意图

3.1 基于BWM计算打击目标价值属性权重

表2 打击目标价值属性集

表3 打击目标价值属性权重值

3.2 基于模糊优选模型计算目标重要性特征值

表4 定性指标的定量化赋值表

表5 打击目标决策属性值

图3 拟打击目标优选排序值

4 结束语

参考文献