基于改进遗传算法的联合作战火力打击计划优化问题研究

刘昊; 张策; 孙奇

doi:10.3969/j.issn.1673-3819.2018.05.003

指挥控制与仿真 >

2018 , Vol. 40 >Issue 5: 11 - 17

DOI: https://doi.org/10.3969/j.issn.1673-3819.2018.05.003

理论研究

基于改进遗传算法的联合作战火力打击计划优化问题研究

刘昊 ,
张策 ,
孙奇

展开

国防大学联合作战学院, 河北石家庄 050000

刘昊(1983-),男,辽宁辽阳人,博士研究生,研究方向为军队指挥学。

张策(1965-),男,博士生导师。

收稿日期: 2018-06-11

修回日期: 2018-07-06

网络出版日期: 2022-05-12

收起

Research on the Improved Genetic Algorithm for improving Joint Firepower Operational Plan

LIU Hao ,
ZHANG Ce ,
SUN Qi

Expand

Joint Operation College of National Defense University, Shijiazhuang 050000, China

Received date: 2018-06-11

Revised date: 2018-07-06

Online published: 2022-05-12

Fold

摘要

针对联合作战中火力打击计划拟制困难的问题,提出一种基于改进遗传算法的联合作战火力打击计划优化方案。通过引入基因群落预评分和多种群并行演化方法重新构造了遗传算法的执行模型,并通过仿真实验验证了方法的有效性。仿真结果表明:该方法确实能够在联合作战筹划阶段实现对火力打击计划的自动优化,相比于标准遗传算法和参谋手工拟制计划具有明显优势。

关键词： 遗传算法; 联合作战; 火力打击计划; 动态火力分配

本文引用格式

刘昊 , 张策 , 孙奇 . 基于改进遗传算法的联合作战火力打击计划优化问题研究[J]. 指挥控制与仿真, 2018 , 40(5) : 11 -17 . DOI: 10.3969/j.issn.1673-3819.2018.05.003

Abstract

Aiming at solving the problems about making joint firepower operational plan difficult, propose a based on improved genetic algorithm solutions. A new method about preliminary ratings of gene community and multiple populations co-evolution are introduced and improved which make a new execution model. Finally, simulation experiments testify the validity of the presented algorithms. The simulations reveal that improving joint firepower operational plan can be realized by this method in operational planning stage. Compared with standard genetic algorithm and manual artificial methods, this method has obvious advantages.

Key words： genetic algorithm; joint operations; firepower operational plan; dynamic weapon-target assignment

在联合作战筹划中,如何高效、科学地拟制联合作战火力打击计划,是战场上能否在有效时间内发挥联合作战诸军兵种部队作战效能的关键因素^[1]。一份优秀的联合作战火力打击计划,能够使诸军兵种部队形成火力打击合力,最大限度地破敌体系,同时均衡分担各部队任务压力,适度留存机动弹药,对于提升部队整体作战能力至关重要,因此联合作战火力打击计划的优化问题成为军事研究的热点。联合作战火力打击计划优化问题的核心在于解决火力分配(Weapon-Target Assignment, WTA)问题,即根据战场实时感知并动态生成的兵力配置表、目标打击表、毁伤能力表,将特定种类和数目的火力打击部队和火力打击目标实施点对点分配,以实现火力打击的过程^[2]。联合火力打击计划优化的难点在于动态火力分配^[3] 的可能性众多,优化计算复杂度高,这是一类典型的有约束组合优化问题,即NP-hard问题^[4],仅靠传统的手工匹配方法无法在给定时间内找到最优计划,必须构造新型算法缩短寻优时间,以便在有限时间内找到相对最优的火力打击计划。

动态火力分配问题最早由Hosein等人提出^[5],目前国内外研究人员已经探索了多种优化方法,应用较多的方法主要有:滚动窗口规划方法^[6]、免疫算法^[7]、神经网络法^[8]、蚁群算法^[9]、粒子群算法^[10]、A*算法^[11]、模拟退火算法^[12]等。上述算法都有各自的理论脉络和算法优势,但从总体看,各算法都存在着某一或某些方面的不足,如算法计算量大、参数调节复杂困难、寻优效率低下、易落入局部最优解、收敛性不强、迁移能力差等问题。相比之下,遗传算法在解决复杂系统寻优问题具有鲁棒、灵活、适应能力强等优点,因此被广泛应用到动态火力分配问题求解中,并取得了不错的效果。标准遗传算法也存在着诸如种群规模大、收敛速度不可控、易于陷入局部最优等问题,针对此类弊端,本文提出了使用基因群落预评分和多种群并行演化方法改进的遗传算法,以提升演化效率和最优个体评估分值,最后通过仿真实验验证了改进遗传算法解决火力打击计划优化问题的可行性和高效性。

1 火力打击计划优化问题描述

火力打击计划优化问题可以分解为拟制、评估、优选3个环节,本文主要研究了如何使用改进遗传算法在众多计划中优选出最优计划,为了进行仿真实验实现优选环节,有必要构建出科学的拟制和简要的评估模型。

1.1 火力打击计划拟制模型介绍

火力打击计划的拟制环节就是利用兵力配置表、目标打击表和毁伤能力表拟制联合作战火力打击计划的过程。为了描述贴合实际,设计作战想定如下:我部担负联合火力打击任务,所属部队包括2个武装直升机中队、3个轰炸机中队、2个常导发射架以及1个远火营(含3个远火连),兵力配置如表1所示。

表1 兵力配置表

编号	名称	类型	打击半径	坐标	可执行任务次数	任务执行时长	任务间隔时长
W101	A飞行中队	武装直升机	100	0*0	2	5	10
W102	B飞行中队	武装直升机	100	0*0	3	5	10
W103	C飞行中队	轰6	250	0*0	2	4	8
W104	D飞行中队	轰6	250	0*0	3	4	8
W105	E飞行中队	歼轰7	250	0*0	2	4	8
W106	A发射架	东风11	330	0*0	2	1	9
W107	B发射架	东风15	330	0*0	4	1	9
W108	A远火连	远火	50	0*0	3	3	5
W109	B远火连	远火	50	0*0	4	3	5
W110	C远火连	远火	50	0*0	3	3	5

当面之敌为蓝军机步旅,正在组织阵地防御,企图扼守主要防御地段,阻我向纵深发展进攻,目标打击表如表2所示。

表2 目标打击表

编号	名称	类型	重要程度	标准毁伤程度	坐标
M101	A指挥所	指挥机构	一级	60%	0*0
M102	B指挥所	指挥机构	一级	60%	0*0
M103	A机场	机场	二级	40%	0*0
M104	B机场	机场	二级	40%	0*0
M105	C机场	机场	二级	40%	0*0
M106	D机场	机场	二级	40%	0*0
M107	E机场	机场	二级	40%	0*0
M108	A防空阵地	防空阵地	二级	40%	0*0
M109	B防空阵地	防空阵地	二级	40%	0*0
M110	C防空阵地	防空阵地	二级	40%	0*0
M111	D防空阵地	防空阵地	二级	40%	0*0
M112	A通信站	通信枢纽	一级	60%	0*0
M113	B通信站	通信枢纽	一级	60%	0*0
M114	C通信站	通信枢纽	一级	60%	0*0
M115	A雷达站	雷达站	一级	60%	0*0
M116	B雷达站	雷达站	一级	60%	0*0
M117	A导弹阵地	地地导弹阵地	二级	40%	0*0
M118	B导弹阵地	地地导弹阵地	二级	40%	0*0
M119	C导弹阵地	地地导弹阵地	二级	40%	0*0
M120	D导弹阵地	地地导弹阵地	二级	40%	0*0
M121	C防空阵地	防空阵地	二级	40%	0*0
M122	D防空阵地	防空阵地	二级	40%	0*0
M123	A通信站	通信枢纽	一级	60%	0*0
M124	B通信站	通信枢纽	一级	60%	0*0
M125	C通信站	通信枢纽	一级	60%	0*0
M126	A雷达站	雷达站	一级	60%	0*0
M127	B雷达站	雷达站	一级	60%	0*0
M128	A导弹阵地	地地导弹阵地	二级	40%	0*0
M129	B导弹阵地	地地导弹阵地	二级	40%	0*0
M130	C导弹阵地	地地导弹阵地	二级	40%	0*0
M131	D导弹阵地	地地导弹阵地	二级	40%	0*0

要求综合计划席参谋根据各部队毁伤能力(表3),拟制联合作战火力打击计划。

表3 毁伤能力表

打击力量类型	打击对象类型	毁伤程度对应出动次数(40%)	毁伤程度对应出动次数(60%)
武装直升机	指挥机构	0	0
武装直升机	机场	0	0
武装直升机	防空阵地	2	4
武装直升机	通信枢纽	1	2
武装直升机	雷达站	1	2
武装直升机	地地导弹阵地	1	2
轰6	指挥机构	1	2
轰6	机场	1	2
轰6	防空阵地	2	4
轰6	通信枢纽	1	2
轰6	雷达站	1	2
轰6	地地导弹阵地	1	2
歼轰7	指挥机构	1	2
歼轰7	机场	1	2
歼轰7	防空阵地	2	4
歼轰7	通信枢纽	1	2
歼轰7	雷达站	1	2
歼轰7	地地导弹阵地	1	2
东风11	指挥机构	0	1
东风11	机场	1	2
东风11	防空阵地	0	1
东风11	通信枢纽	0	1
东风11	雷达站	1	2
东风11	地地导弹阵地	1	2
东风15	指挥机构	0	1
东风15	机场	1	2
东风15	防空阵地	0	1
东风15	通信枢纽	0	1
东风15	雷达站	1	2
东风15	地地导弹阵地	1	2
远火	指挥机构	1	2
远火	机场	2	4
远火	防空阵地	1	2
远火	通信枢纽	1	2
远火	雷达站	1	2
远火	地地导弹阵地	1	2

综合计划席受领任务后,应第一时间依据指挥员决心意图为目标清单实施打击先后排序,而后分析我现有火力打击力量的特点,并根据火力打击能力表为各参战部队赋予火力打击任务,最后汇总生成联合作战火力打击计划,见表4。

表4 初始火力打击计划

序号	突击目标	毁伤程度	使用部队	执行任务次数	突击时间
0	M121	40%	W110	1	T+0~T+3
1	M102	60%	W110	1	T+8~T+11
2	M104	40%	W104	1	T+0~T+4
3	M104	40%	W107	1	T+0~T+1
4	M113	60%	W110	1	T+16~T+19
5	M106	40%	W104	1	T+12~T+16
6	M102	60%	W103	1	T+0~T+4
7	M101	60%	W105	1	T+0~T+4
8	M127	60%	W108	1	T+0~T+3
9	M110	40%	W102	1	T+0~T+5
10	M107	40%	W108	1	T+8~T+11
11	M101	60%	W102	1	T+15~T+20
12	M101	60%	W105	1	T+12~T+16
13	M114	60%	W107	1	T+10~T+11
14	M112	60%	W103	1	T+12~T+16
15	M103	40%	W108	1	T+16~T+19
16	M117	40%	W109	1	T+0~T+3
17	M105	40%	W107	1	T+20~T+21
18	M111	40%	W101	1	T+0~T+5
19	M101	60%	W106	1	T+0~T+1
20	M131	40%	W110	1	T+24~T+27
21	M116	60%	W104	1	T+24~T+28
22	M117	40%	W105	1	T+24~T+28
23	M130	40%	W110	1	T+32~T+35
24	M120	40%	W108	1	T+24~T+27
25	M118	40%	W105	1	T+36~T+40
26	M107	40%	W109	1	T+8~T+11
27	M128	40%	W102	1	T+30~T+35
28	M129	40%	W110	1	T+40~T+43
29	M103	40%	W106	1	T+10~T+11

1.2 火力打击计划评估模型介绍

为了实现火力打击计划的优选,本文构建出简易的火力打击计划评估模型,主要设计了如下评估指标:

1)火力打击执行时长指标(T);

2)各部队出动次数指标(C);

3)目标重要程度指标(Z);

4)完成任务情况指标(W)。

评估过程可描述为:

设共有m支参与火力打击的部队,对n个目标实施火力打击;选取第i支部队对各目标实施火力打击,共执行k_i次打击任务,当前敌第j个目标。设第i支部队单次执行任务时长为u_i,任务间隔时长为v_i;则火力打击执行时长评估指标T的计算公式为

(1)T=min

100, 2000 m a x (k i (u i + v i) - v i)

设第i支部队可执行火力打击任务的总次数为s_i次;则各部队出动次数评估指标C的计算公式为

(2)C=min

100, ∑ i = 0 m 100 (s i - k i) m · s i

设目标打击清单中只包含一、二级目标,一级目标数目为h,火力打击计划中对一级目标实际打击的数目为p;则对目标打击的重要程度评估指标Z的算法描述如图1所示。

显示原图|下载原图ZIP|生成PPT

图1 重要程度评估指标Z算法描述图

设对第j个目标实施火力打击的总时长为o_j;则完成任务情况评估指标W的算法描述如图2所示。

显示原图|下载原图ZIP|生成PPT

图2 完成任务评估指标W计算流程图

满足约束条件:目标坐标必须在对该目标执行火力打击任务的部队射程内,如不在射程内则去除该项打击任务。设第i支部队的打击半径为b_i,坐标为(xm_i,ym_i);准备打击第j个目标的坐标为(xn_j,yn_j)。约束公式如下:

(3)b_i≥

(x m i - x n j) 2 + (y m i - y n j) 2

综合评估得分F为各指标的经验加权求和,计算公式为

(4)F=

T · 3 + C + Z + W · 5 10

以表X火力打击计划为例,计算评估过程如下:

1)计算火力打击执行时长指标T。根据表X计算出各部队执行时长为{5,35,16,28,40,11,21,27,11,43},根据公式(1)可计算出T=46.51分。

2)计算各部队出动次数指标C。根据表X计算出各部队出动次数k_i为{1,3,2,3,4,2,3,4,2,6},查兵力配置表得到火力打击总次数s_i为{2,3,2,3,2,2,4,3,4,3},m=10,根据公式(2)可计算出C=-15.83分。

3)计算目标重要程度指标Z。首先根据表X确定各目标的打击先后排名,第一名排名31,而后依次递减,各目标按打击先后排序为{6,2,12,3,14,5,9,0,0,8,15,11,4,10,0,17,13,20,0,19,1,0,0,0,0,0,7,21,22,18,16};各目标实际排名分值=245分;最佳排名分值=231.4分;根据图1可计算出Z=100分。

4)计算完成任务情况指标W。根据火力计划确定执行该计划后对各目标完成任务情况为{100,100,100,100,100,100,100,0,0,50,50,50,50,100,0,50,100,100,0,100,100,0,0,0,0,0,50,100,100,100,100},各目标实施火力打击的时长为{20,11,9,4,1,4,3,0,0,5,5,4,3,1,0,4,28,4,0,3,3,0,0,0,0,0,3,5,3,3,3},则根据图2可计算出Z=51.61分。

5)计算综合评估分值F。根据公式(4)可计算出F=48.27分。

2 改进遗传算法原理

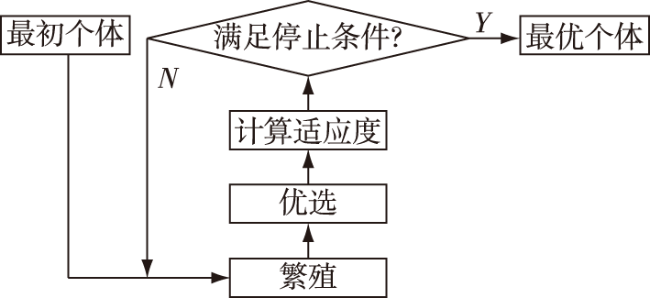
2.1 标准遗传算法介绍

遗传算法是由美国Michigan大学的John Holland与其同事于1975年首先提出,该算法是一种借鉴生物演化规律而设计的随机搜索方法,从自然生态系统中生物对外界环境的复杂适应过程入手,模拟生物进化机制创造人工的生物演化进程,进而构造出人工的生物演化系统模型^[13]。由于遗传算法简单易用,鲁棒性好,具有强有力的全局搜索能力,且算法简单、易于编程,目前已经成为一种解决众多实际优化问题的有效工具^[14]。

标准遗传算法是将优化问题同生物个体建立对应关系,将问题中的优化参数用基因编码替代,进而将优化问题映射为生物群体中找最优个体的过程。而后利用基因突变、有性繁殖、适应评估、优选下一个个体等过程建立生物演化循环,使种群不断演化,种群内的最优个体评分分值逐渐趋向于最优解^[15]。具体算法描述如下:

1)设置初始个体。随机生成一个初始个体,本文中可表示为一套具体的联合作战火力打击计划(如表4)。将火力计划的每行子任务描述为一个基因,则多个基因共同组成了初始个体。图3表示初始个体结构,个体由基因、寿命、评估分值组成。

显示原图|下载原图ZIP|生成PPT

图3 初始个体结构图

2)繁殖为新种群。通过基因突变、两性基因交换和两性基因拆补使最初个体自我繁殖,扩充为1000个个体。设个体A_m和个体A_n在第k位上对应的基因分别为a_mk和a_nk,b取[0,1]之间的随机整数,b=0表示基因不交换,b=1表示基因交换;则交换的具体方法为:

(5)第k位基因

A m : a m k (1 - b) + a n k b A n : a n k (1 - b) + a m k b

设基因拆补为将a_mk拆下,插补到a_nk后,b=0表示基因不拆补,b=1表示基因拆补;则拆补的具体方法为:

(6)第k位基因

A m : a m k (1 - b) A n : a m k b

3)计算种群中个体的评估分值。按照火力打击计划评估模型对每个个体计算评估分值,分值越高表示该个体在群体中的适应性越强。

4)优选个体。使用轮盘法在种群中优选出100个个体,使高评分个体有较大概率留存,低评分个体也有小概率的留存机会。同时删除寿命达到上限的个体(留存超过5代个体),防止超级个体破坏种群基因多样性。设第i个体评分分值为F_i,p_i表示个体被选中的概率;轮盘法的算法描述:

(7)p_i=

F i ∑ i = 1 n F i

5)演化终止条件判断。如满足“种群优选个体高低分差为<0.5”条件,则退出循环,输出最佳结果;否则执行2)。

显示原图|下载原图ZIP|生成PPT

图4 遗传算法基本流程图

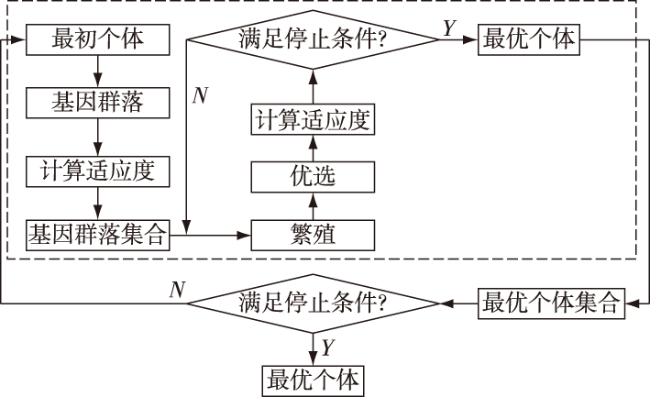
2.2 改进遗传算法介绍

虽然标准遗传算法为解决火力打击计划优化问题提供了可行性解决方案,但它还存在两个不容忽视的缺陷:未成熟收敛和遗传后期的收敛迟滞,前者影响算法精确度,后者影响算法执行效率。为此,本文采用基因群落预评分和多种群并行演化的方法改进标准遗传算法,具体改进说明如下。

1)基因群落预评分

标准遗传算法的基因变异的随机发生的,不存在方向可控性,而实际经验告诉我们,绝大多数的基因变异对种群演化是无意义的,因此在基因概念基础上,引入基因群落概念。基因群落由几个基因聚集组成,可完成一项独立功能,如在联合作战火力打击计划的优化问题中,基因代表了“某一时刻由某一部队打击某一目标”,基因群落则由多个相同部队基因组成,代表了“整个火力打击过程中某一部队打击了哪些目标”,简而言之,基因群落是由一支部队能够执行的火力打击任务序列构成,如图5所示。则对火力打击计划的总体评分,可拆解为对各基因群落的单独评分之和,而对基因群落的预先评分可以有效剔除标准遗传算法随机产生的低评分基因群落。

显示原图|下载原图ZIP|生成PPT

图5 基因群落示意图

2)多种群并行演化

标准遗传算法由于演化效果的不确定性,导致每次演化产生的最优个体评估分值都不相同,因此考虑在单种群演化基础上,引入多种群并行演化概念。设有多个种群互不干扰的独立演化,则会产生多个互相独立的最优个体,在时间条件允许情况下,取各种群产生的最优个体中的最高评估分值个体为最终输出结果。多种群并行演化体现了以降低算法效率提升算法精确度的思想,即“多次重复演化,取最优结果”。

改进的遗传算法执行步骤(见图6)如下:

1)设置最初个体。

2)设置基因群落集合。对每支部队能够打击到的目标产生对应的基因群落,并对每个群落计算群落评分,优选高评分的基因群落组成基因群落集合。

3)繁殖为新种群。将变异对象从基因变异改为从基因群落集合中随机选取一支部队的基因群落,其他同标准遗传算法。

4)计算种群中个体的评估分值。

5)优选个体。

6)演化终止条件判断。

7)重复演化。将最优个体存入最优个体集合,判断时间是否允许,如允许则返回1)重复演化;否则退出循环,输出最优个体集合中的最高分个体。

显示原图|下载原图ZIP|生成PPT

图6 改进遗传算法基本流程图

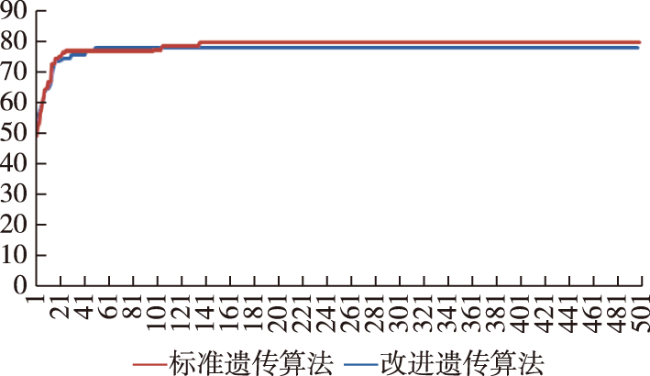
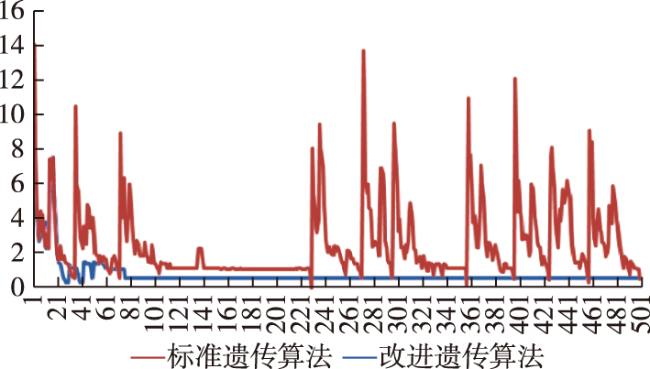
3 仿真实验结果分析

仿真实验环境设置如下:设定每代种群上限1000个,优选种群为100个;变异发生概率为每个新个体可随机产生1次基因突变;遗传终止条件为优选个体总最高低分差值小于0.5(意味着种群中所有个体分值都演化为最高分值)。本文实验计算机配置:联想笔记本电脑运行程序,配置:Intel酷睿双核CPU T7300 2.0 GHz;3G内存;32位Win7操作系统;vc6.0编程环境。为验证改进遗传算法的有效性,选取标准遗传算法作为参考对象,在实验过程中,两种算法的控制参数相同,包括种群规模、变异概率、遗传终止条件等。

图7中为两种算法对比的实验结果,其中横坐标表示演化代数,纵坐标表示各代最优个体分值。从图中可以看出,随着演化代数的增多,两种算法都收敛到最高分值,但改进遗传算法的收敛分值略高于标准遗传算法的收敛分值,并且收敛曲线更加平滑,不存在明显波动,证明改进遗传算法能突破局部最优解限制,在多次重复演化中逼近全局最优解。

显示原图|下载原图ZIP|生成PPT

图7 各代演化中最优个体分值比较

图8中为两种算法各代高低分差对比结果,其中横坐标表示演化代数,纵坐标表示各代最高分值个体和最低分值个体的高低分差。从图中可以看出,随着演化代数的增多,标准遗传算法的高低分差逐渐归于0,在各代演化中并无明显波动,演化计算逐渐趋向于无意义的时间消耗;而改进遗传算法采用了多种群并行演化策略,各代高低分差具有周期性归于0的波动特点,算法通过一次次的演化寻找全局最优解。从实验结果可以得出结论:在时间允许的情况下,改进遗传算法具备无限逼近全局最优解的能力,而标准遗传算法可能陷入局部最优解。

显示原图|下载原图ZIP|生成PPT

图8 各代高低分差比较

表5中为两种算法各代时间消耗对比结果,在演化代数相同的前提下,标准遗传算法平均每代演化用时0.98 s,改进遗传算法平均每代演化用时0.76 s,改进遗传算法每代演化的平均用时明显低于标准遗传算法。从实验结果可以得出结论:基因群落预评分能够有效缩短演化时长,提升遗传算法的演化效率,提速比例可达28.9%。

表5 时间消耗比较/s

	标准遗传算法	改进遗传算法
总代数	500	500
总用时	442	332
平均每代用时	0.98	0.76

表6为以表4为初始火力打击计划,经过改进遗传算法演化产生的最优火力打击计划。可以看出,相比于传统手工制作的火力打击计划而言,改进遗传算法生成的火力打击计划任务执行时长更短、各部队任务分配更均匀、对目标体系破坏性更强、预留弹药更合理、综合评估分值更高。对比结果如表7所示。

表6 改进遗传算法生成最优火力打击计划

序号	突击目标	毁伤程度	使用部队	执行任务次数	突击时间
0	M103	40%	W103	1	T+0~T+4
1	M120	40%	W108	1	T+0~T+3
2	M104	40%	W104	1	T+0~T+4
3	M105	40%	W105	1	T+0~T+4
4	M106	40%	W105	1	T+12~T+16
5	M107	40%	W103	1	T+12~T+16
6	M108	40%	W108	1	T+8~T+11
7	M109	40%	W109	1	T+0~T+3
8	M110	40%	W110	1	T+0~T+3
9	M111	40%	W108	1	T+16~T+19
10	M117	40%	W102	1	T+0~T+5
11	M101	60%	W107	1	T+0~T+1
12	M113	60%	W106	1	T+0~T+1
13	M118	40%	W102	1	T+15~T+20
14	M119	40%	W109	1	T+8~T+11
15	M121	40%	W110	1	T+8~T+11
16	M123	60%	W107	1	T+10~T+11
17	M125	60%	W107	1	T+20~T+21
18	M122	40%	W109	1	T+16~T+19
19	M128	40%	W110	1	T+16~T+19
20	M112	60%	W106	1	T+10~T+11
21	M102	60%	W106	1	T+20~T+21
22	M129	40%	W101	1	T+0~T+5
23	M131	40%	W104	1	T+12~T+16

表7 初始计划和最优计划对比

指标项	初始计划	最优计划
执行时长指标T	46.51	95.23
出动次数指标C	-15.83	6.76
重要程度指标Z	100	100
完成任务指标W	51.61	80.64
综合评估指标F	48.27	79.66

4 结束语

本文针对联合作战火力打击计划优化中的动态火力分配问题,提出使用改进遗传算法自主生成最优火力打击计划的方法。该方法创新点主要有:提出用遗传算法的思路解决联合作战火力打击计划的优化问题,并设计简易的火力打击计划评估模型验证方法可行性;通过设计基因群落预评分机制,实现对无意义的基因突变的过滤,提升了遗传算法的执行效率;通过设计多种群并行演化机制,有效地克服了遗传算法早熟缺陷。实验表明,将该方法应用到联合作战火力打击计划优化操作中,能有效提高火力打击计划拟制的针对性和时效性。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序

[1]	叶征. 信息化作战概论[M]. 北京: 军事科学出版社, 2007.

[2]	刘新华. 作战辅助决策与军事系统工程[M]. 北京: 海潮出版社, 2007.

[3]	张滢, 杨任农, 左家亮. 改进分解进化算法求解动态火力分配多目标优化模型[J]. 兵工学报, 2015, 36(8):1533-1540.

[4]	Lioyd S P, Witsenhausen H S. Weapon allocation is NP-complete[C]. Reno,NV,US:IEEE, 1986:1054-1058.

[5]	Hosein P A, Athans M. Preferential defense strategies,part II: the dynamic case, LIPS-P-2003[R]. Cambridge.UK: MIT. 1990.

[6]	Lee Z J, Lee C Y, Su S F. An immunity-based ant colony optimization algorithm for solving weapon-target assignment problem[J]. Applied Soft Computing, 2002, 2(1):39-47. DOI

[7]	阮旻智, 李庆民, 刘天花. 编队防空火力分配建模及其优化方法研究[J]. 兵工学报, 2010, 31(11): 1525-1529.

[8]	Mori S, Nisbihara H, Furuta K. Control of unstable mechanical System-control of pendulum[J]. Int J Control, 1976, 23:673-692. DOI

[9]	Zhang J, Wang X, Xu C. ACGA algorithm of solving weapon-target assignment problem[J]. Open Journal of Applied Sciences, 2003, 2(4):74-77. DOI

[10]	Leboucher C, Shin H S. Novel evolutionary game based multi-objective optimisation for dynamic weapon target assignment[C]. Cape Town. South Africa: IFAC. 2014:3936-3941.

[11]	汪定伟, 王俊伟, 王洪峰. 智能优化算法[M]. 北京: 高等教育出版社, 2007.

[12]	贺小亮, 毕义明. 基于模拟退火遗传算法的编队对地攻击WTA建模与优化[J]. 系统工程与电子技术, 2014, 36(5): 900-904.

[13]	马亚龙. 评估理论和方法及其军事应用[M]. 北京: 国防工业出版社, 2013.

[14]	Deb K, Pratap A, Agarwal S. A fast and elitist multiobjective genetic algorithm:NAGA-II[J]. Evolutionary Computation, IEEE Transations on, 2002, 6(2):182-197.

[15]	王小平, 曹立明. 遗传算法理论、应用与软件实现[M]. 西安: 西安交通大学出版社, 2002.

Options

文章导航

模态框（Modal）标题

摘要

本文引用格式

Abstract

1 火力打击计划优化问题描述

1.1 火力打击计划拟制模型介绍

表1 兵力配置表

表2 目标打击表

表3 毁伤能力表

表4 初始火力打击计划

1.2 火力打击计划评估模型介绍

图1 重要程度评估指标Z算法描述图

图2 完成任务评估指标W计算流程图

2 改进遗传算法原理

2.1 标准遗传算法介绍

图3 初始个体结构图

图4 遗传算法基本流程图

2.2 改进遗传算法介绍

图5 基因群落示意图

图6 改进遗传算法基本流程图

3 仿真实验结果分析

图7 各代演化中最优个体分值比较

图8 各代高低分差比较

表5 时间消耗比较/s

表6 改进遗传算法生成最优火力打击计划

表7 初始计划和最优计划对比

4 结束语

参考文献