1 引言
1.1 传感器网络数据采集
1.2 轨迹优化算法
2 系统模型及问题形式化
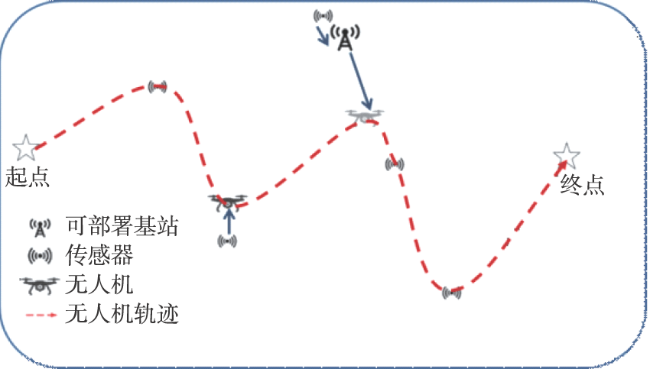
2.1 系统模型
2.2 问题形式化
3 算法设计
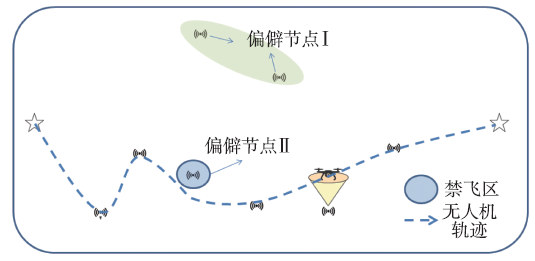
3.1 偏僻节点筛选算法
| 算法1 偏僻节点筛选算法 |
|---|
| 1:初始化系统参数,设置筛选阈值为threshold1; 2:求解TSP问题,得到访问顺序; 3:预筛选‖Q0-wu‖≥threshold1,u→G; 4: G→g,$\mathcal{U}$-g→G; 5:代入集合G,求解(P); 6:比较无人机飞行距离,得到偏僻节点集合$\mathcal{M}$。 |
3.2 联合优化算法
| 算法2 求解(P1)的块坐标下降算法 |
|---|
| 1:初始化系统参数,筛选偏僻节点,设置迭代精度为tol; 2:初始化W0,计算初始无人机轨迹Q0, r←0; 3:更新迭代次数r=r+1; 4:将Wr、Qr代入(P2)得到Ar+1; 5:将Ar+1、Qr和Wr代入式(P4),获得Qr+1; 6:将Ar+1、Qr+1和Wr代入式(P5),得到Wr+1; 7:直到满足收敛条件。 |
3.3 收敛性分析
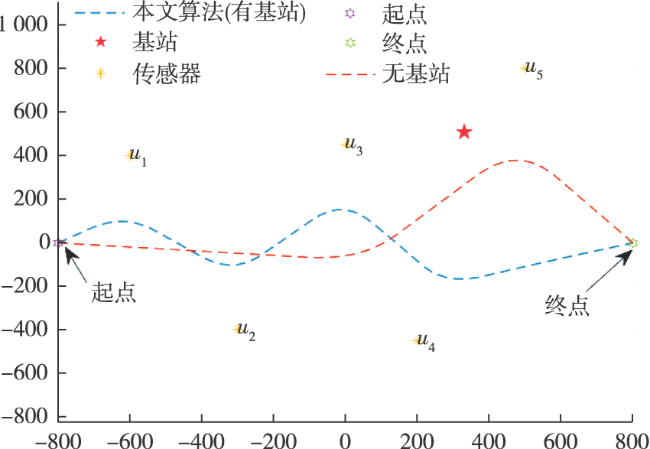
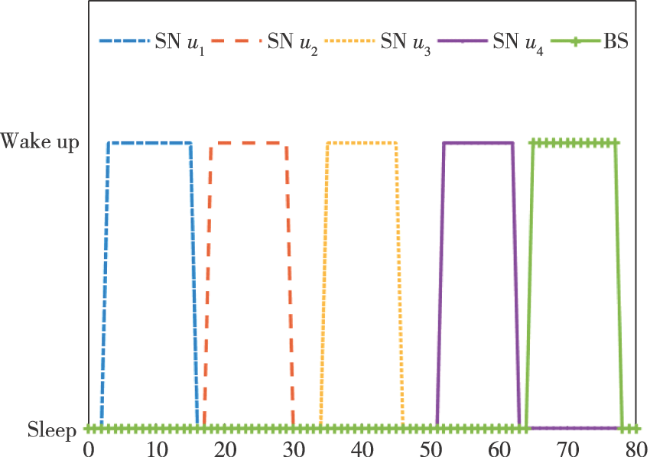
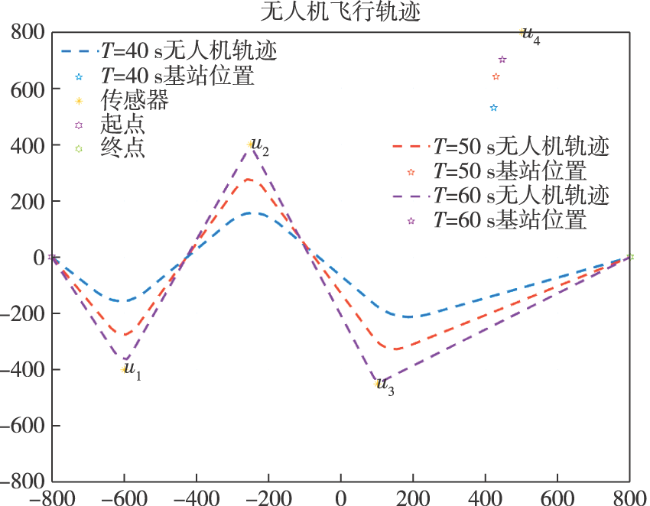
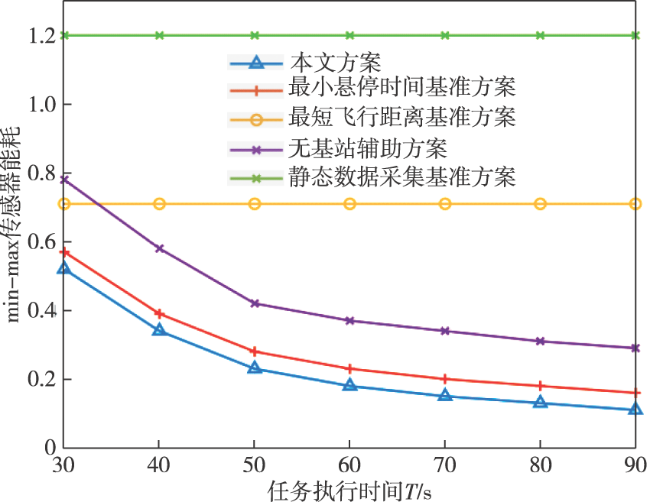
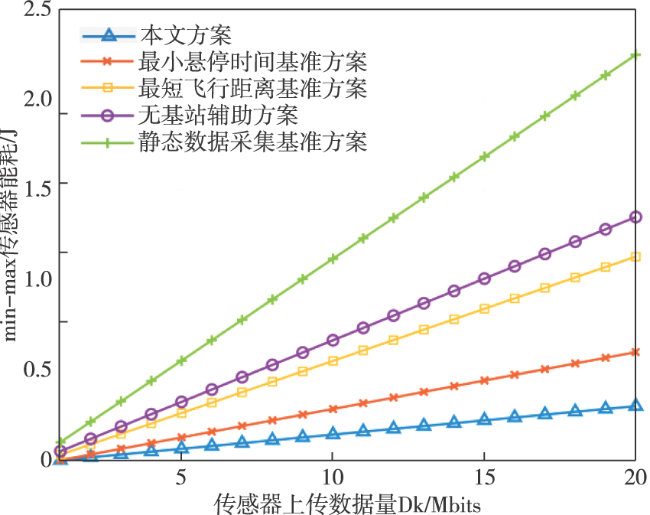
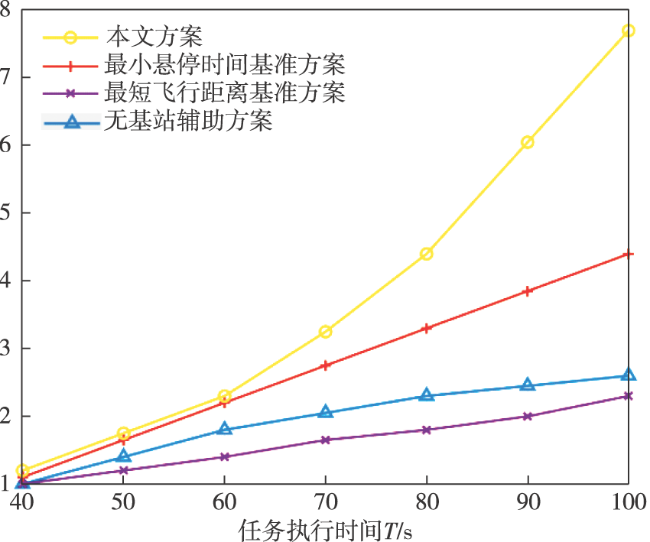
4 仿真分析
表1 仿真参数 |
| 参数 | 数值 |
|---|---|
| 无人机飞行高度 | H=50 m |
| 路径损耗指数 | α=2 |
| 无人机最大飞行速度 | Vmax=50 m/s |
| 通信带宽 | B=1 MHz |
| 噪声功率 | =-110 dBm |
| 1 m处的信道功率增益 | β0=-60 dB |
| 传感器发射功率 | Pu=0.1 W |
| 可部署基站发射功率 | PBS=0.2 W |

 中国指挥与控制学会会刊
中国指挥与控制学会会刊