中国科技核心期刊      中国指挥与控制学会会刊     军事装备类重点期刊
指挥控制与仿真

指挥控制与仿真 >

2020 , Vol. 42 >Issue 1: 64 - 69

DOI: https://doi.org/10.3969/j.issn.1673-3819.2020.01.013

理论研究

一种八关节串联机器人的运动学解析分析及仿真

  • 刘梓阳 ,
  • 徐大林 ,
  • 孙宏伟
展开
  • 江苏自动化研究所, 江苏 连云港 222061

作者简介：刘梓阳(1995—),男,河南温县人,硕士研究生,研究方向为机器人运动控制。

徐大林(1964—),男,研究员。

Copy editor: 张培培

收稿日期: 2019-05-21

  修回日期: 2019-06-10

  网络出版日期: 2022-05-19

收起

Kinematics Analysis and Simulation of a Eight-joint Tandem Robot

  • LIU Zi-yang ,
  • XU Da-lin ,
  • SUN Hong-wei
Expand
  • Jiangsu Automation Research Institute, Lianyungang 222061, China

Received date: 2019-05-21

  Revised date: 2019-06-10

  Online published: 2022-05-19

Fold

摘要

多关节机器人运动学分析是研究机器人学的重要内容。多于六自由度的串联机器人运动学因其运动学反解的不唯一性一直是国内外机器人技术研究的重点之一。针对多关节机器人逆运动学反解困难问题,传统大都采用神经网络等优化方法求解,这些方法存在运算量大、准确度低等问题。结合一种实际应用的八关节串联机器人结构和工作特性,提出一种几何法和解析法相结合的多关节机器人逆运动学新算法并进行仿真验证。首先根据机器人结构建立D-H模型并确定机器人结构参数,对机器人正逆解进行分析解算,最后,以Matlab为仿真工具验证解算结果的正确性与准确程度,为冗余自由度串联机器人的改进、设计及应用等方面提供了一种新的思路。

关键词： 多关节机器人; 机器人运动学; 机器人仿真

本文引用格式

刘梓阳 , 徐大林 , 孙宏伟 . 一种八关节串联机器人的运动学解析分析及仿真[J]. 指挥控制与仿真, 2020 , 42(1) : 64 -69 . DOI: 10.3969/j.issn.1673-3819.2020.01.013

Abstract

Kinematics analysis of multi-joint robot play an important part in robotics research. Because of the nonuniqueness of its inverse solution, robot kinematics with more than 6 freedom degrees is still the focuses of the research. For the inverse kinematics problem, some optimization methods,like neural network, are mostly used. These methods have many problems such as heavy calculation and low accuracy. In this paper, a new inverse kinematics algorithm based on geometric and analytical methods is proposed and verified by simulation. The D-H model is established according to the robot structure and the structure parameters of the robot are determined. The positive and negative solutions of the robot are analyzed and calculated. Finally, Matlab is used as the simulation tool to verify the correctness and accuracy of the results. It provides a new idea for the improvement, design and application of the robot with more than 6 axises.

Key words： multi-joint robot; robot kinematics; robot simulation

机器人逆运动学是机器人进行路径规划和运动控制的基础[1]。传统对六自由度机器人的运动学研究已较为成熟[2],而对具有冗余自由度(超过6个空间运动自由度)的机器人运动学研究仍处于摸索阶段[3]。从传统的机器人学角度,冗余自由度串联机器人的正向运动学相对比较容易处理,但逆运动学因其空间自由度较多,无法获得唯一解。传统逆运动学解算方法不唯一,主要分为数值法和解析法。数值法解算步骤复杂,需要依赖大量的数值迭代运算。例如Koker[4]等人设计多个Elman神经网络来进行冗余机器人的逆运动学运算,并采用遗传算法对关节角度的求解精度进行优化。北京航空航天大学机器人研究所[5]针对九自由度的“5R+4T”混联机器人,提出了一种单一约束条件下,利用反变换法和逆矩阵特征,得到九自由度机器人的正反解。这些方法大都是建立在优化模型基础上,应用智能化方法求解的思路,但也存在过拟合、可靠性低等共性问题,无法从根本上对具有冗余自由度机器人的多个逆解的结果进行优化量化。
本文针对一种典型的串联八自由度机器人系统的机构特点提出几何法和解析法相结合的运动学方法,在解析模型的基础上,简化了多关节机器人的解算步骤和解算复杂程度。

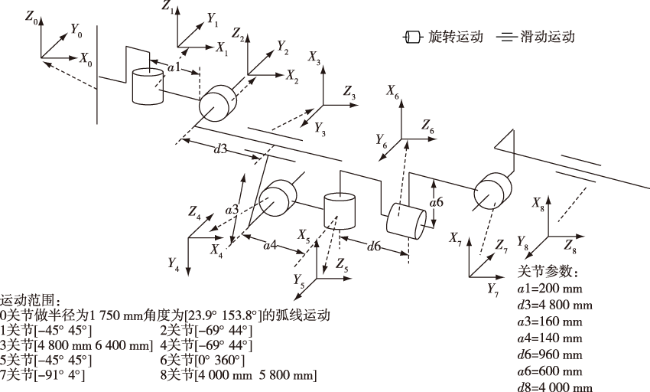
1 机器人模型建立

本文以钻孔机器人图1a)为例,根据机器人结构如图1b),做出结构模型简图如图2,然后使用D-H法确定各关节DH变换参数[6]。
图1 机器人及八百由度结构图
图2 坐标系结构简图
在机器人坐标系结构简图中,基准坐标系{0}在关节变量θ=0时与坐标系{1}重合,末端工具坐标系{8}建立在机器人末端。
根据机器人结构参数可以确定机器人连杆参数和变量,如表1所示。
表1 八自由度机器人连杆参数表
坐标系i 连杆夹角
θi/(°)		 连杆距离
Di/mm		 连杆长度
ai-1/mm		 连杆扭矩
αi-1/(°)		 运动范围
0 0 0 0 0 为机器人基座,做弧线运动,与坐标系{1}重合
1 0 0 0 0 [-45° 45°]
2 -90 0 200 -90 [-69° 44°]
3 0 4 800 160 -90 [0 mm 1 600 mm]
4 90 0 0 90 [-69° 44°]
5 -90 260 140 90 [-45° 45°]
6 -90 960 0 -90 [0° 360°]
7 0 0 600 90 [-91° 4°]
8 0 4 000 0 -90 [0 mm 1 800 mm]

2 机器人运动学分析

2.1 机器人正向运动学分析

根据DH法,第i关节坐标系相对于第i-1关节坐标系的变换矩阵为
i i - 1T= c o s ( θ i ) - s i n ( θ i ) 0 a i - 1 s i n ( θ i ) c o s ( α i - 1 ) c o s ( θ i ) c o s ( α i - 1 ) - s i n ( α i - 1 ) - d i s i n ( α i - 1 ) s i n ( θ i ) s i n ( α i - 1 ) c o s ( θ i ) s i n ( α i - 1 ) c o s ( α i - 1 ) d i c o s ( α i - 1 ) 0 0 0 1
规定正弦和余弦简化表达形式如下
si=sin(θi),ci=cos(θi),sij=sin(θi+θj),cij=cos(θi+θj),(i,j=1,2,…)
将钻臂各参数代入式(1),可得钻臂各连杆坐标变换矩阵
1 0T= c 1 - s 1 0 0 s 1 c 1 0 0 0 0 1 0 0 0 0 1 2 1T= c 2 - s 2 0 200 0 0 1 0 - s 2 - c 2 0 0 0 0 0 1
3 2T= 1 0 0 0 0 0 1 d 3 0 - 1 0 0 0 0 0 1 4 3T= c 4 - s 4 0 160 0 0 - 1 0 s 4 c 4 0 0 0 0 0 1
5 4T= c 5 - s 5 0 140 0 0 - 1 - 260 s 5 c 5 0 0 0 0 0 1
6 5T= c 6 - s 6 0 0 0 0 1 960 - s 6 - c 6 0 0 0 0 0 1
7 6T= c 7 - s 7 0 600 0 0 - 1 0 s 7 c 7 0 0 0 0 0 1 8 7T= 1 0 0 0 0 0 1 d 8 0 - 1 0 0 0 0 0 1
将每个相邻变换矩阵依次相乘就可以得到钻臂运动学方程
8 0T= 1 0T 2 1T 3 2T 4 3T 5 4T 6 5T 7 6T 8 7T
钻臂的运动学研究与其他类型的机器人运动学研究相同,在求出机器人的运动学方程之后,只需要将各时刻关节变量的值代入公式(2)中,即可求出各时刻末端执行机构的位置和姿态[7]。

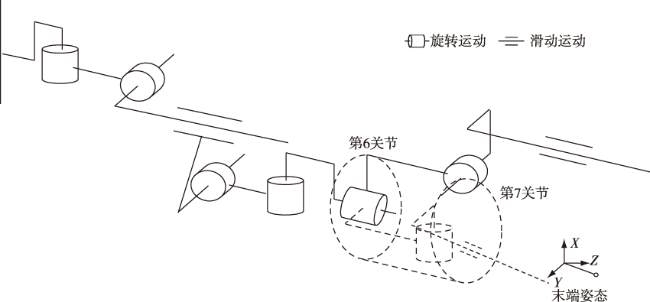
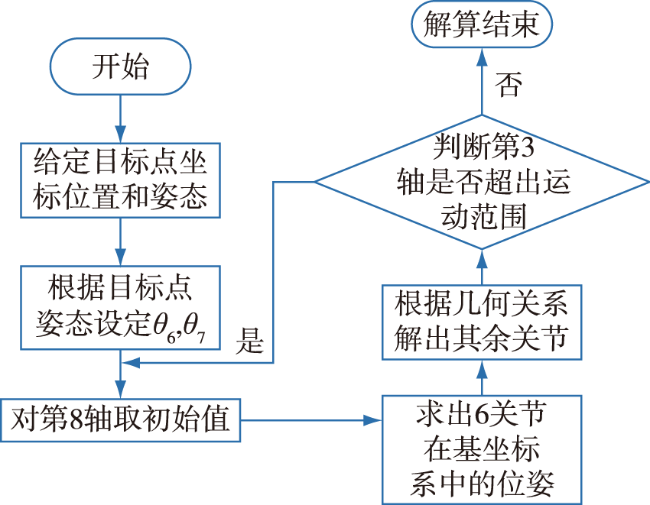
2.2 机器人逆向运动学分析

在冗余自由度串联机器人运动学中,更需要关注的是机器人的逆向运动学分析[8]。相比于机器人运动学正解,机器人运动学逆解的解析结果不具备唯一性,可能存在多解情况,在机器人的实际工作中,往往需要找出一组最合适的逆解。因此,在求解过程中可以根据机器人的结构特点对机器人进行一些关节限制来求取最优解。
根据机器工作原理,首先给定机器人末端执行机构的位姿矩阵和工作孔的摆角。机器人末端位置可由位置空间确定,机器人末端姿态可由姿态空间确定。位置空间由1个可活动基座以及基座相连的5个关节的可达范围组成,姿态空间由末端3个关节的可达范围组成。工作孔的摆角方向和大小由第6、7关节实现,因此在求解运动学逆解的过程中θ6,θ7可以提前确定,如图3所示。
图3 摆角实现方式
运动学逆解的求解过程如下。
1)对于给定的末端位置(p80x,p80y,p80z),姿态(n8,s8,a8),可以写出末端坐标系的状态矩阵
T= n 80 x o 80 x a 80 x p 80 x n 80 y o 80 y a 80 y p 80 y n 80 z o 80 z a 80 z p 80 z 0 0 0 1
已知θ7,并根据机器人距离工作点距离将d8设定一个初始长度,可求得

8 6T= 7 6T 8 7T=

c o s ( θ 7 ) 0 - s i n ( θ 7 ) 600 - d 8 s i n ( θ 7 ) 0 1 0 0 s i n ( θ 7 ) 0 c o s ( θ 7 ) d 8 c o s ( θ 7 ) 0 0 0 1

由式(3)和式(4)可以求出第6坐标系在基坐标系中的位姿
6 0T= c 6 c 15 - s 6 c 15 - s 15 200 c 1 + 160 c 1 c 2 - 960 s 15 - d 3 c 1 s 2 + 140 c 1 c 6 s 15 - s 6 s 15 c 15 200 s 1 + 160 s 1 c 2 + 960 c 15 - d 3 s 1 s 2 + 140 s 1 - s 6 - c 6 0 - 160 s 2 - d 3 c 2 + 260 0 0 0 1=T( 9 6T)-1
2)根据上式可知θ1+θ5,由第6坐标系在基坐标系中的几何关系可求θ1,θ2,d3
θ1=arctan(( 6 0T(2,4)-960·cos(θ1+θ5))/( 6 0T(1,4)+960·sin(θ1+θ5)))
B=( 6 0T(2,4)-960·cos(θ1+θ5)-340·sin(θ1))/sin(θ1)
C= 6 0T(3,4)-260d3= ( B 2 + C 2 - 160 2 )
θ2=arctan((160·C+d3·B)/(d3·C-160·B))
至此可求出θ1,θ2,d3,因θ2+θ4=0,可求出q4=-q2,q5=arccos(q1+q5)-q1。
由于d8为初始值,所以求出d3可能会超出可达范围,若超出范围,则需要调整d8重新计算,直至所有关节变量都在运动范围内,计算流程如图4所示。
图4 逆解计算流程图

3 机器人运动学仿真

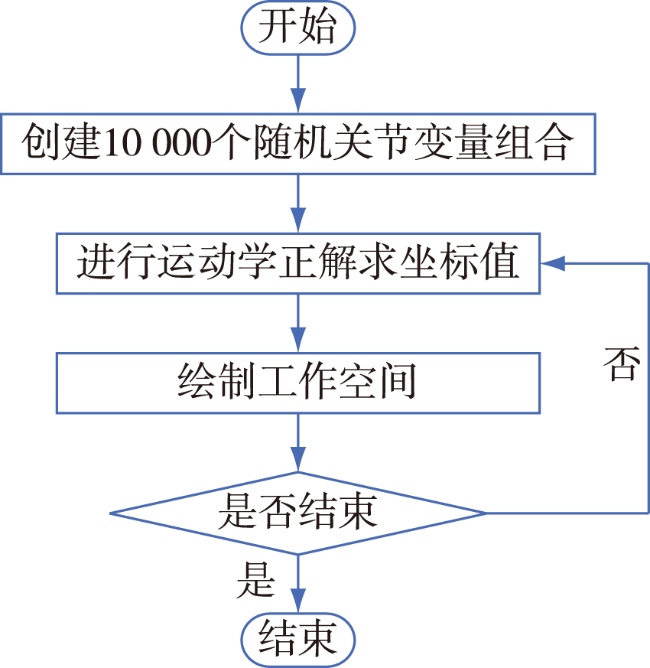
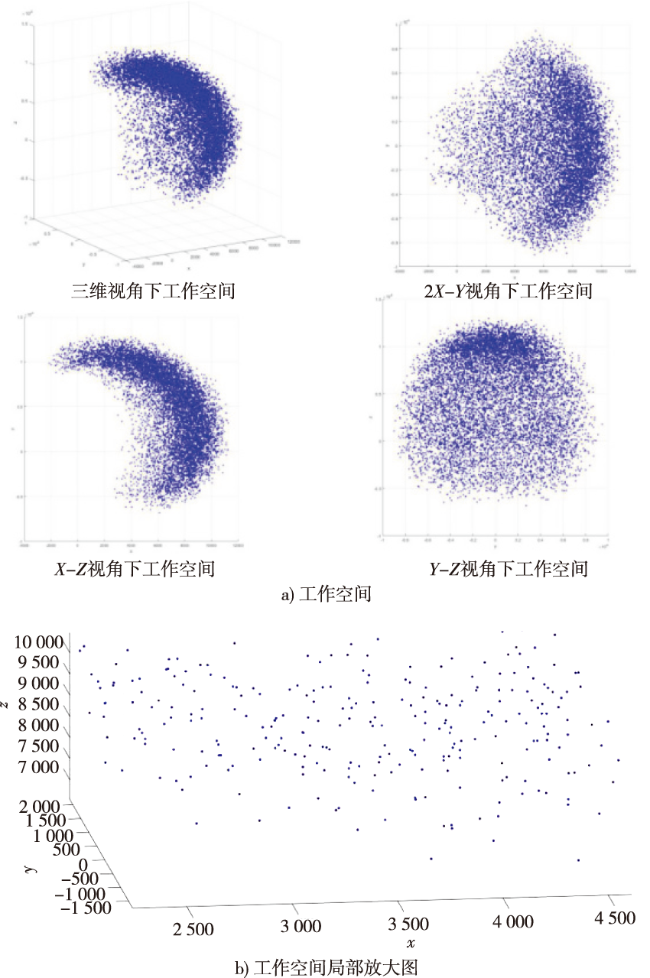
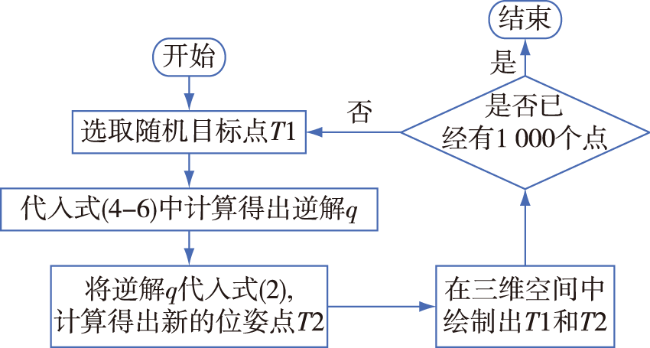
在对钻孔机器人运动学正反解理论研究之后,本文通过Matlab仿真平台对分析结果进行验证[9],可以方便有效地得出验证结果,并通过可视化的方式将验证结果展示出来。

3.1 机器人工作空间仿真

机器人工作空间的求解是机器人运动学正解的一部分[10],机器人的工作空间是机器人末端(坐标系{8}的原点)在基坐标系(坐标系{0})中所能达到的空间位置点所组成的集合。可以通过在机器人关节可达范围内随机选取关节值,各关节运动范围如表2,进行正解运算并通过Matlab求解出机器人的工作空间,工作空间仿真流程如图5所示。
表2 机器人各关节运动范围
关节
1 2 3 4 5 6 7 8
运动
范围		 [-45° 45°] [-159°-46°] [4 800 mm
6 400 mm]		 [-21° 134°] [-135°-45°] [-90° 270°] [-91° 4°] [4 000 mm
5 800 mm]
图5 工作空间仿真流程
对随机选择的10 000个点进行正解运算后的结果在三维坐标系表示出来如图6所示。
图6 工作空间和工作空间局部放大图
由图6可以看出,机器人工作空间为弧面,符合机器人的实际工作情况,随机选取的点越多,描述的工作空间越准确。

3.2 机器人逆解验证

为了验证机器人逆解分析的正确性和准确度,本节通过在工作空间内随机选取1 000个实例点进行验证。首先将随机选取的目标点位姿作为给定位姿,通过Matlab逆解运算,可以解出一组合适的关节变量,将这组关节变量重新进行正解运算,可以得到一组新的位姿矩阵,将新的位姿矩阵与给定的位姿矩阵进行对比,就可以验证该反解方法的准确性,验证流程图如图7所示。
图7 逆解验证流程图
验证完成后的结果描述在三维坐标系中如图8所示。
图8 逆解验证结果及局部放大图
在1000个逆解验证结果中,蓝色“+”表示给定位姿,绿色“.”表示解算后新的位姿。逆解误差如表3所示。
表3 逆解结果误差
逆解误差
位置误差/mm 姿态误差/mm
最大值 2.33×10-5 3.15×10-11
最小值 8.92×10-13 5.76×10-17
平均值 3.41×10-7 8.56×10-13
由仿真结果图和误差表中可以看出,这种解析算法的精确度可以满足机器人的工作需要。每个目标点的逆解只有一个,说明该机器人在实际工作中每个目标点逆解是唯一的。

4 结束语

本文结合机器人结构特点和运动特性,提出了一种解析法和几何法相结合的八关节机器人运动学解析方法,为多关节冗余自由度机器人运动学解析提供了一种新思路。算法的仿真结果表明该方法拥有较高的准确度,满足机器人的工作需要,为机器人轨迹规划、运动控制等进一步研究提供有力支持。

参考文献

原文顺序 | 文献年度倒序 | 文中引用次数倒序
[1]
GUO Dongsheng, ZHANG Yunong. Li-function Activated ZNN with Finite-time Convergence Applied to Redundant Manipulator Kinematic Control Via Time-varying Jacobian matrix pseudoinversion[J]. Applied Soft Computing, 2014, 24(11):158-168.

DOI

[2]
刘亚军, 黄田. 6R操作臂逆运动学分析与轨迹规划[J]. 机械工程学报, 2012, 48(3): 9-15.

[3]
姜宏超, 刘士荣, 张波. 六自由度模块化机械臂的逆运动学分析[J]. 浙江大学学报, 2010, 44(7):1348-1354.

[4]
KOKE R R, CAKAR, SARI T, et al. Neural-network Committee Machine Approach to the Inverse Kinematics Problem Solution of Robotic Manipulators[J]. Engineering with Computers, 2014, 30(4):641-649.

DOI

[5]
张帆, 刘达, 王田苗. 九自由度混连微创外科机器人的正反解[J]. 北京航空航天大学学报, 2011, 12(4):447-451.

[6]
马江. 六自由度机械臂控制系统设计和运动学仿真[D]. 北京: 北京工业大学, 2012.

[7]
林海峰, 王姮. 多关节机器人工作空间仿真方法[J]. 微型机与应用, 2014, 33(2):72-74.

[8]
徐俊虎, 栾楠, 张诗雷, 等.7 自由度机械臂的运动学逆解与优化[J]. 机电一体化, 2011(6):28-33.

[9]
周群海, 王兆辉. 6R关节式机器人运动学仿真分析[J]. 组合机床与自动化加工技术, 2018, 11(11):63-66.

[10]
田海波, 马宏伟, 魏娟. 串联机器人机械臂工作空间与结构参数研究[J]. 农业机械学报, 2013, 44(4):196-201.

Options
文章导航

/

〈 〉